Thin films provide a rich setup that is of interest from multiple points
of view. From application side, these thin films and their instabilities
are of relevance to a number of fields that rangefrom glass making to semiconductor
and polymer applications, solar cells, to mention just a few fields of
applications. From modeling side, thin films are demanding due
to the presence of multiple spatial and temporal scales and due to the
need to incorporate multi physics that is often of relevance in particular
in the setups involving spreading and instabilities of thin films on substrates.
Recent group activities on the topic of Newtonian thin films have focused on
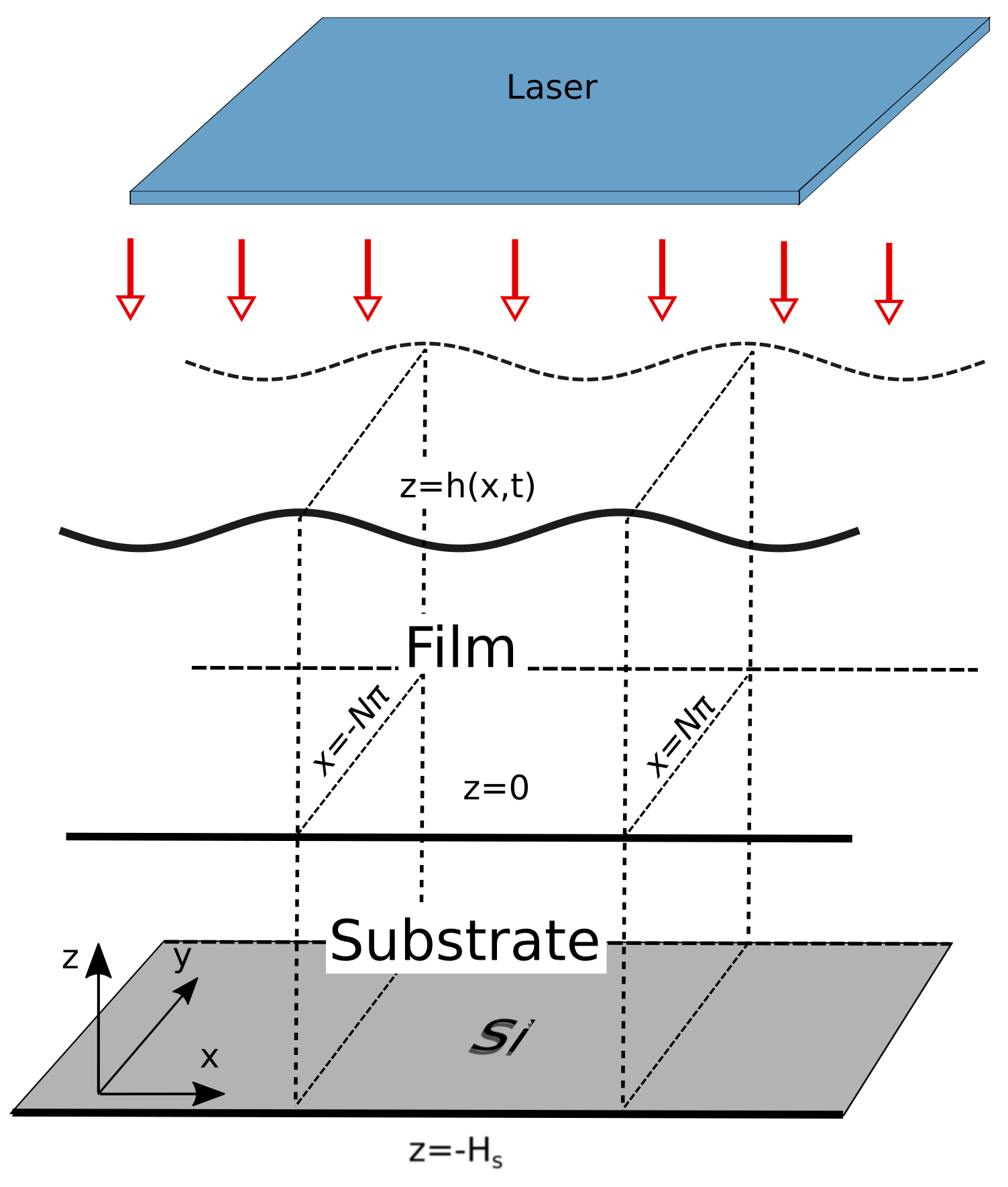
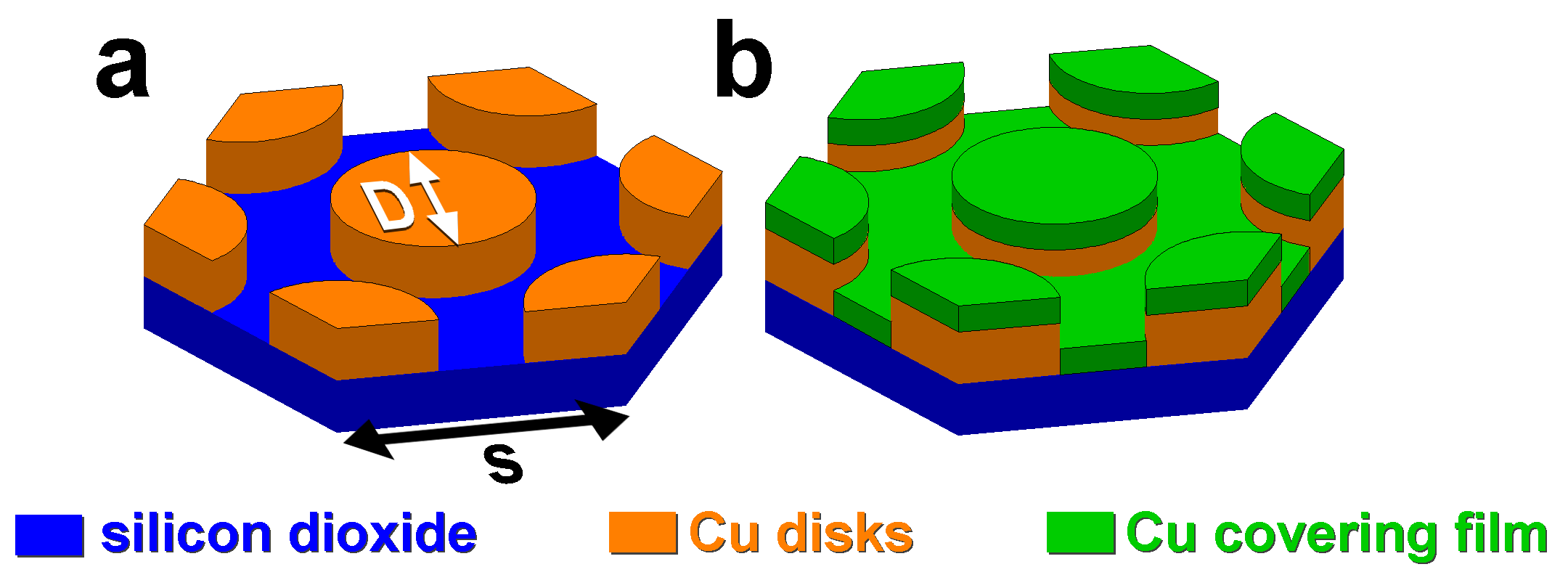
modeling and simulations of metal films of nanoscale thickness exposed to laser
radiation, in collaboration with the experimental group at U. Tennessee and Oak
Ridge National Laboratory. Metal films are relevant to a number of technological
fields with applications that include plasmonics, magnetic nanoparticles, control
surface optical properties, catalysts for nanowire growth and many others. In many of
these fields ordered arrays of nanoparticles are needed. While in liquid phase, the film
instabilities lead to such arrays via self- or directed- assembly, and we are interested
in the basic mechanisms that are relevant to the instabilities.
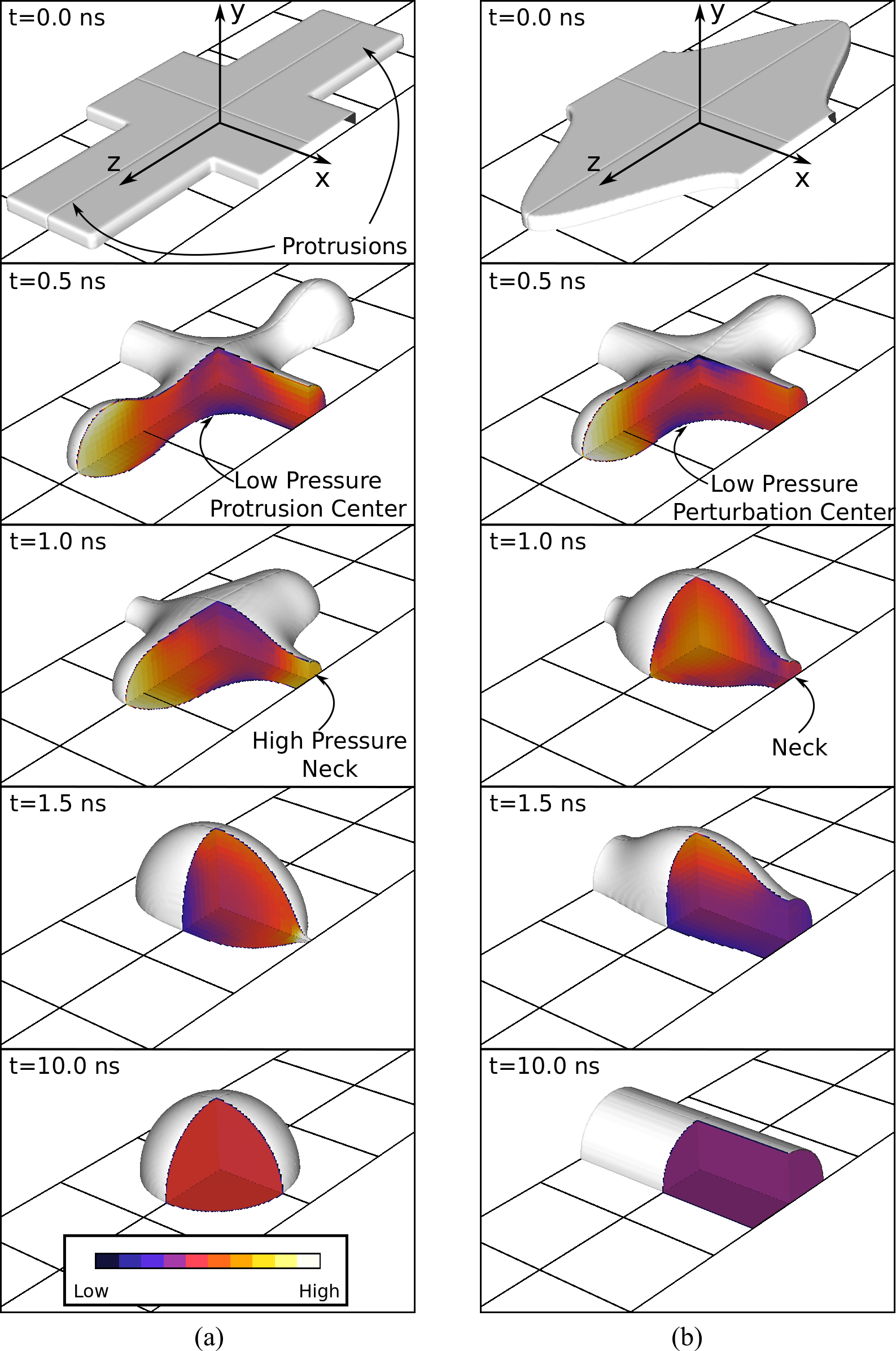
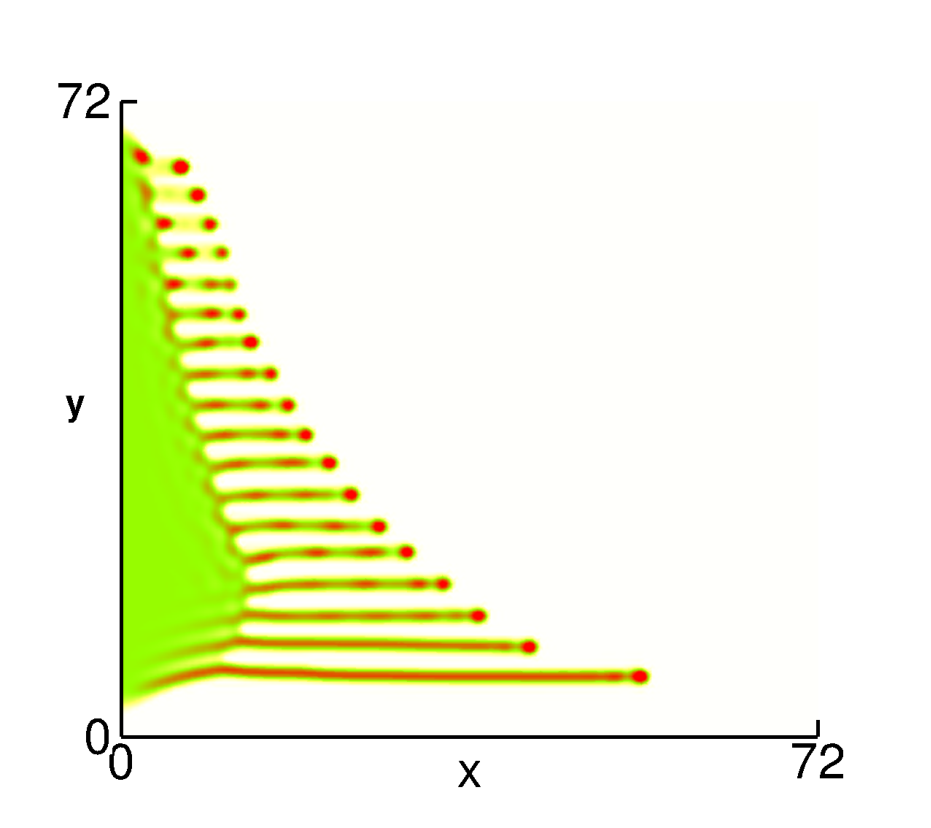
At NJIT, we have carried extensive simulations of
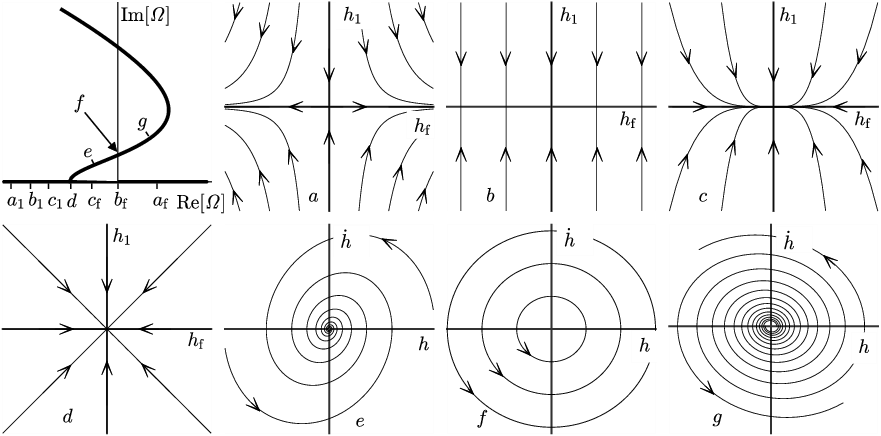
thin metal films within the long-wave model that reduces the problem to solving
a nonlinear 4th order evolution equation of diffusion type, as well as by directly
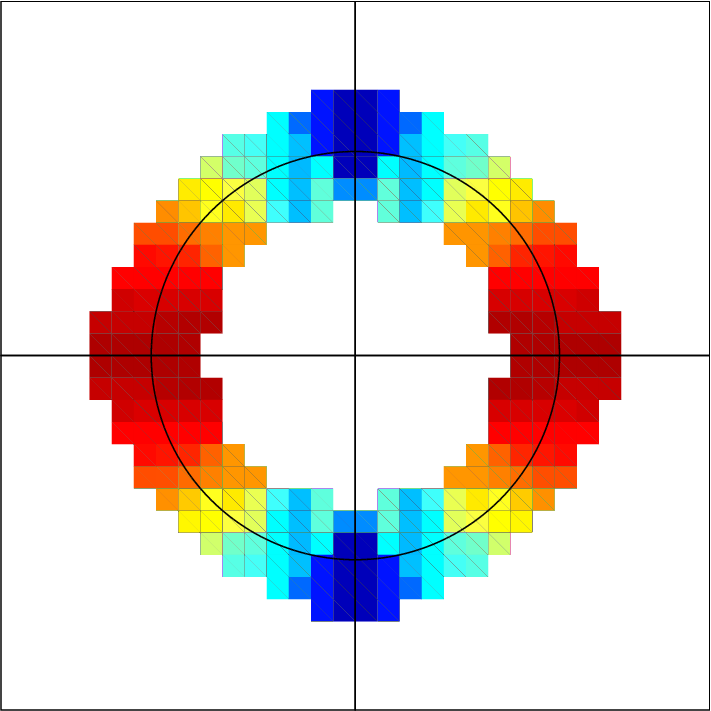
solving Navier-Stokes equations using Volume-of-Fluid method. A number of new
and interesting results has been obtained, including much better understanding of
the connection between film instability and its geometry, of the influence of
fluid/solid interaction forces, heat flow through the film and the substrate, to name
just a few aspects.
Earlier works on thin films include a variety of configurations and setups including
considerations of stochastic effects, flows down an incline, hanging and evaporating films, among others.
Some of the considered configurations were also explored in research projects including
undergraduate students in the Capstone Laboratory [link to the capstone page].
The relevant recent publications can be found below, and older works are listed at the
publication list or
here.
We acknowledge past and current support by NSF and Fulbright Foundation.