Projects

Modeling Frosting Utilizing Monte Carlo Simulations

Instructor: Lou Kondic

Lab Assistant: Joseph D'Addesa

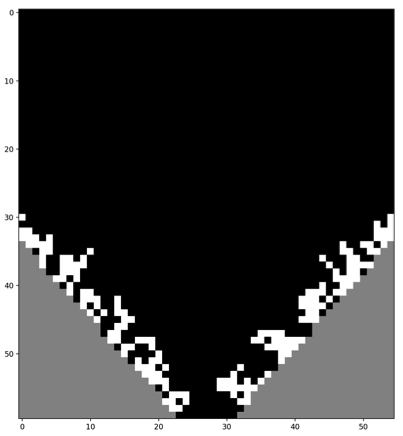
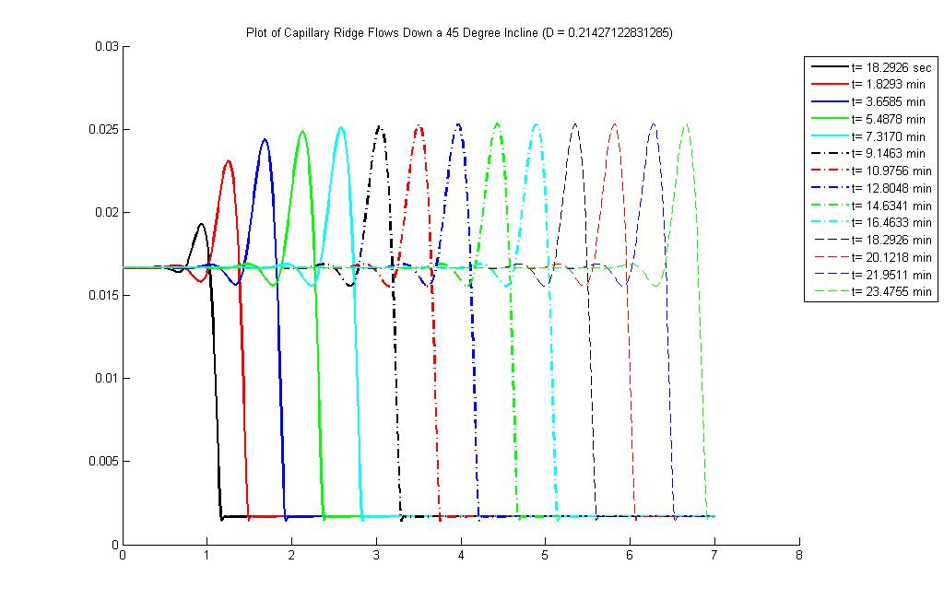
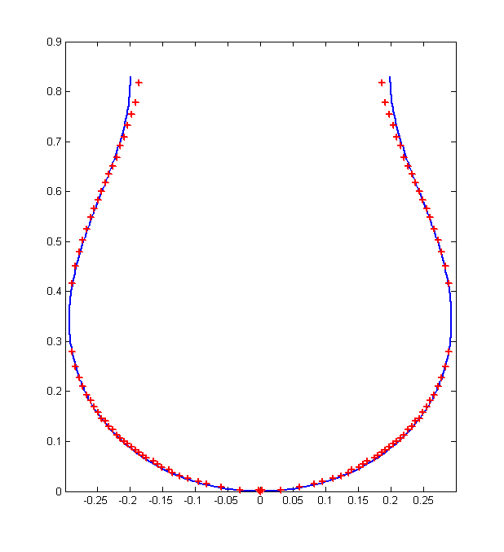
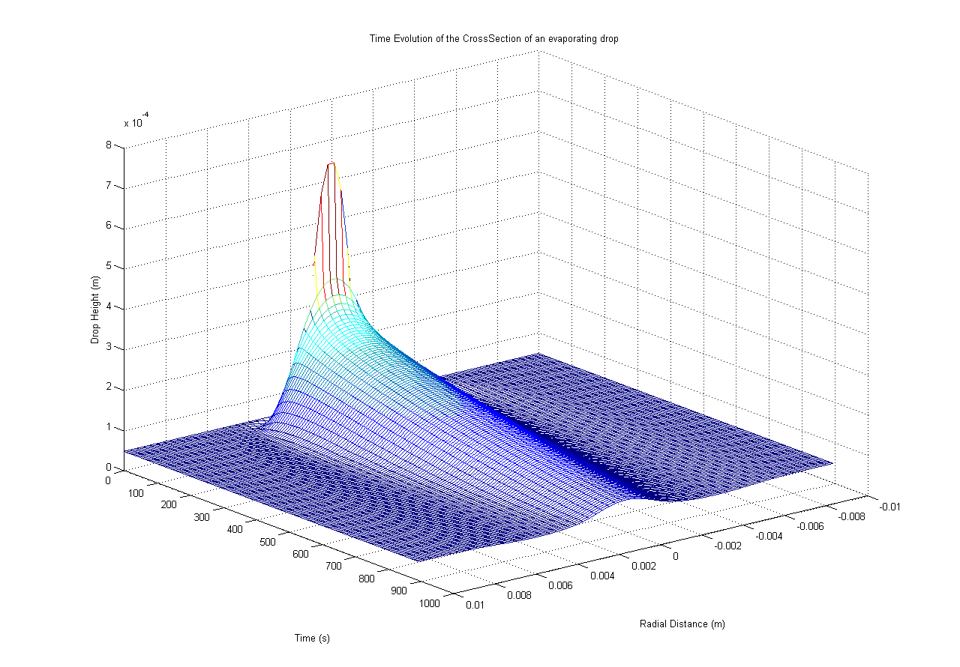
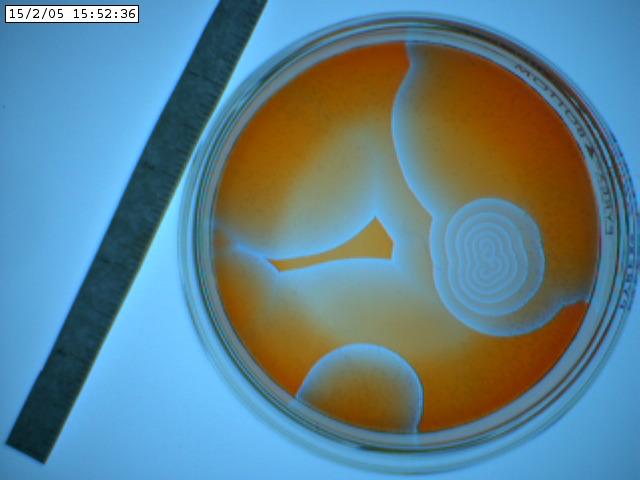
This Capstone project focuses on modeling frosting on microstructured substrates in experiments carried out by instructors' collaborators at the Max-Plank Institute of Polymer Science in Mainz, Germany. Figure 1 shows few examples of experimental images of frost spreading in experiments carried out at different humidities (From Phys. Rev. E 104, 044901 (2021)). Based on the experimental results and helped by direct communication with the researchers involved in carrying out these experiments, the students formulated Monte Carlo-based simulations of the frosting process, focusing in particular on the correlation of the outcome of the results (such as the fractal dimension of the emerging patterns) between the experiments and simulations.

We thank Lukas Hauer (at Helmholtz University Berlin as of 2023) for help with the interpretation of experimental results and useful discussions.

Computational Topology Methods Applied to Pore-based Filters

Instructor: Lou Kondic

Lab Assistant: Joseph D'Addesa

This Capstone project focuses on the application of computational topology to the networks formulated by our current PhD candidate Matt Illingworth (in collaboration with our former student Binan Gu). Such networks (see Figure 1, from J. Membrane Sci. 657 120668 (2022))) are used as a proxy for filters used in applications. The focus of the project is on computing topological measures describing the geometry of the pore networks. The students have carried out such computations and have also learned about the basics of computational topology. The resulting measures quantifying the geometry of the networks are then compared to the filtration performance.

We thank Binan Gu (at WPI as of Spring 2023) and PhD student Matt Illingworth (Department of Mathematical Sciences, NJIT) for providing network data and helping with data processing.

This project is supported in part by the NSF Grant No. DMS - 2201627.

Computational Topology Methods Applied to Particulate Systems

Instructor: Lou Kondic

Lab Assistant: Joseph D'Addesa

This Capstone project focuses on the analysis of the structure and interparticle interaction in the experiments carried out by the instructor's collaborators in 2022 at U. Stuttgart, Germany, using XRCT (X-ray computed tomography) (PNAS 120, 2219999 (2023)). The experiments focus on the mechanical response of glass-rubber particle systems, with the goal of understanding how the addition of rubber particles modifies this response. Figure shows an experimental image with the glass particles in blue, and rubber particles in red. Participating students analyzed the data using two types of approaches emerging from persistent homology. The first approach is based only on the geometry of packings and quantifies this geometry using so-called alpha-complexes. The second approach considers particle interactions (quantified by their distance) in addition to the geometry. The outcome of the topology-based approaches was compared to experimentally measured mechanical properties, and suggestions for future experiments were formulated.

We thank Kianoosh Taghizadeh from the University of Twente, Netherlands for sharing the experimental data and Rituparna Basak (PhD, NJIT Department of Mathematical Sciences) for helping with data processing.

This project is supported in part by the NSF Grant No. DMS - 2201627.

Frost spreading on micro-structured substrates: modeling and Monte-Carlo simulations

Frost nucleation and spreading on solid surfaces is a common process which is very much of interest and often concern in everyday life. While this process is difficult to quantify on unstructured surfaces, growth of frost on microstructured surfaces is easier to quantify and model. Recent works have considered frosting on such surfaces experimentally. One novel finding is that there are different regimes of frost growth, characterized by surface temperature and the amount of humidity. In particular, for an intermediate humidity regime, frost growth appears to be fractal. The NJIT component of the project focusses on formulating an appropriate model for frost growth, and on using such a model to set up Monte-Carlo simulations of frost spreading. The ultimate goal is to formulate a model that would allow to understand a transition between different regimes and to check whether the fractal-like patterns observed in experiments are indeed fractal and if so, to find their fractal dimension. Figure shows an example of Monte-Carlo simulations of frost growth.

We thank to Prof. Doris Vollmer from MPI for Polymer Research, Mainz, Germany, for bringing this problem to our attention, and to Lukas Hauer from the same institution for helping supervise the student project at NJIT.

Healing of thin films: hole closing under vibrations

This project focuses on understanding the influence of vibrations on closing of a hole in a thin film. The project was inspired by recent experiments which explored hole closing and in particular the self-similar regime describing hole radius as a function of time. The project component at NJIT considers theoretical and computational aspects of the problem, and in particular focuses on formulating the governing partial differential equation for the film thickness. The participating students have worked on the project jointly with the lab assistant Joseph D'Addesa, for whom this project is a part of his PhD research. Figure shows an example of drop spreading used as a test problem. .

We thank to Prof. Steffen Hardt from TU Darmstadt, Germany, for bringing this problem to our attention.

Acousto-fluid dynamics: driving thin films by an applied acoustic field

Acoustic waves is known to influence fluid motion. This project's focus in on the results of recent experiments showing that acoustic driving can be used to produce spreading of fluids on substrates. The component of the project at NJIT considers theoretical and computational aspects, and in particular focuses on formulating a model describing coupling of fluid motion and an applied acoustic field, as well as on developing appropriate computational methods for solving the nonlinear partial different equation governing the fluid motion. The participating students have worked on the project jointly with the lab assistant Joseph D'Addesa, for whom this project is a part of his PhD research. Figure illustrates an example of a numerical solution showing flow of a thin film over an obstacle. The numerical code used is deposited at GitHub. We thank our collaborators, Profs. Linda Cummings (NJIT), Javier Diez (UNCPBA, Argentina), and Ofer Manor (Technion) for insightful discussions.

Nonlinear long water waves

The students have developed numerical models using a finite difference method to solve the weakly nonlinear Boussinesq model (a system of two nonlinear PDEs describing the free surface motions in shallow water) with various types of boundary conditions. Their numerical solutions have been compared with available experimental data. Specific research projects include (1) the generation of solitary waves by lifting a gate at the end of a 2-D wave tank; (2) the generation of periodic waves by a piston-type wave maker; (3) the resonant generation of solitary waves by a disturbance moving with a near-critical speed; (4) the propagation and deformation of a single solitary wave over bottom topography.

Study of Impact of Molten Wax Droplets on Substrates

This capstone project was dedicated to the solidification and impact of a wax drop impacting a solid surface. In a first part, we established a 1D solidification model, derived from the Stefan problem and energetic arguments, that aimed at predicting the experimental observations. We then carried out experiments to study the parameters that determined the dynamics of droplets of paraffin wax impinging and freezing on a metal and a glass surface. The impacts were photographed and the spreading of the splat formed after freezing was measured. Photographs showed liquid wax droplet recoiling in the center followed by the solidification. By comparing to the simple model, we found that the early stage solidification did not affect the drop impact. A simple model was then used to predict the number of azimuthal instabilities that grew at the rim of the spreading drops upon impact. Future study will consider the contact line effects.

Thin film flow inside a funnel

This Capstone projects focuses on the problem of analysis of converging flows, such a flow on the inside of a funnel. Figure shows an example of a physical experiment where thin film is released close to the upper edge of a funnel, and then let to evolve. While this setup is related to a number of classical problems involving thin films, it introduces a novel twist related to converging nature of the flow. The participating students have carried out four separate but related projects (i) physical experiments, image analysis, and quantification of the instabilities that develop during the flow; (ii) asymptotic analysis, (iii) numerical simulations, and (iv) self-similar type of analysis of a simplified setup. The direct comparison between experimental, analytical, and numerical results allowed to the participating students to develop better understanding of fluid instabilities, and, more broadly, of the techniques used in applied mathematics research.

The instructor thanks to Joshua Dijksman (Wageningen University, The Netherlands) for significant help with the experimental aspects of the project, and to Te-Sheng Lin (National Chiao Tung University, Taiwan) for his support with numerical and analytical aspects. Combined experimental theoretical study was published in J. Fluid Mechanics (2021). This project was supported by NSF Grants No. CBET-1604351 and DMS-1815613.

Numerical Study of the Instability of Miscible and Immiscible Thin Fluid Layers on Substrates

This capstone project involves the study of the fluid dynamical problem of thin bilayer films. There has been a recent experimental study on the Ag-Au bimetallic nanoparticles produced by the laser dewetting of Ag/Au bilayer films on a substrate. The aim of this activity here is to develop a physical understanding of final properties of bimetallic systems, and to enhance the knowledge of the structure and morphology of the nanoparticles. Of particular focus of this study here is to analyze the differences in the composition and the final size distribution of the nanoparticles using direct numerical simulations. While there are many parameters involve in the problem setting, here we only focus on changing the relative thickness of each layer, changing the relative viscosity of each layer, as well as relative viscosity of the surrounding, and finally varying the equilibrium contact angle.

Stochastic Modeling of Porous Media Flow

This project focuses on reproducing and improving the model of multilayered membrane filters, developed by Ian Griffiths (J. Membrane Sci. 511, 108 (2016)). The model focuses on creating an innovative method of membrane filtration by carrying out stochastic simulation of the particles transport through the multilayered filter and entrapment of particles within. Here, the filters are composed of a number of membrane layers stacked on top of each other. Each membrane layer is characterized by a two dimensional array of pores with given initial radii and a taper angle which prescribes a difference in pore radii between successive layers. Figure 1, from the reference above, illustrates the membrane geometry. The participating students have developed their own simulations of the flow through a multilayered filter, and have been successful in reproducing the results from the Griffiths work. This project was continued in direct collaboration with Dr. Griffiths (Oxford University, UK) in the direction of carrying out simulations of filters characterized by random pore structure. The project was supported by NSF Grant No. DMS-1615719.

Modeling of Connected Branched Membrane Filters

The previous work has focused on unconnected membrane morphology, as illustrated in Fig. 1c The current project has focused on computing the performance of filters characterized by different membrane structures, as shown in Figs. 1a and 1b, and comparing them with the performance of the membranes characterized by unconnected membrane structure. To carry out this comparison, an elaborate branching model has been developed, and simulations have been formulated and carried out. The focus of these simulations has been on computing throughput for the membrane structures shown in Fig. 1 and discussing which of the configurations is optimal. Furthermore, the project involves considering asymmetric membranes, where pores are perturbed by random noise. The question here is how random perturbations, that are expected in applications, influence membrane performance. The project has been continued after the end of semester, leading to a publication in J. Fluid Mechanics (2020) . The project was supported by NSF Grant No. DMS-1615719.

Stochastic Modeling of Porous Media Flow

This project focuses on the modeling of filtration mechanism via stochastic Monte-Carlo type of simulations. Here, filtration process is modeled via random walkers which stick to the membrane walls if their random motion brings them to the vicinity of the membrane walls. Random walks continue until clogging of the pore. The particular aspect of the problem that the project focused on was the influence of the pore shape on throughput (how many particles managed to pass through a pore) and on time of clogging. Figure shows an example of the simulations. The students have found out that a large number of simulations is needed to reduce statistical effects and have therefore put together scripts that allowed them to carry out thousands of simulations of clogging progress. The outcome was then compared to the continuum model results that had been developed previously. This project continued as a summer research project for one of the participating students, Catherine Sousa. The project was supported by NSF grant No. DMS - 1615719 and by the NJIT provost fellowship.

Breakup of a filament

The breakup of viscous filaments has, and is being studied experimentally, theoretically, and numerically. In this study, we focus on the breakup of finite size liquid filaments on substrates, using direct numerical simulations. Although there are many parameters involved when determining whether a liquid filament breaks up, we illustrate the effects of three parameters: Ohnesorge number, the ratio of the viscous forces to inertial and surface tension surfaces, the liquid filament aspect ratio, and a measure of the fluid slip on the substrate, i.e. slip length. Through these parameters, we are able to determine whether a liquid filament breaks up into one or multiple droplets or collapse into a single droplet on the substrate. We compare our results with the results for free standing liquid filaments. We show that the presence of the substrate promotes breakup of the filament. We also discuss the effect of the degree of slip on the break up. We comprehensively explore the parameter domain regions when including the slip effects. Partial support by NSF-CBET-1604351 is acknowledged.

Impact on Granular Matter

Impact on dense gravitationally compacted assemblies of particles leads to complex dynamics of the impactor and of the granular particles themselves. The details of the intruder's dynamics, and of the causal connection between this dynamics and the material response has been a subject of extensive research during the last decade. In this project, we use topological tools to analyze the results of physical experiments carried out with photoelastic particles at Duke University. Photoelasticity allows to visualize (using high-speed imaging) the structure of the force/stress field in the granular assembly during impact. Novel computational topology methods allow for quantification of the force/stress field that develops during an impact. Such quantification has been carried out, leading to much better understanding of the particulate material response to impact. The Capstone project has continued into a summer research project for one of the participating students, Tadanaga Takahashi, supported by an NSF REU supplement. The instructor acknowledges useful input by Abe Clark, PhD, Yale University, and by the collaborating groups from Rutgers and Duke Universities, let by Profs. K. Mischaikow and R. Behringer, respectively.

Particulate Matter: Percolation, Persistence, Topology

Particulate systems are of relevance in a number of different fields, from granular matter to suspensions and bacterial colonies. This project focuses on particulate assemblies exposed to compression. When compression is sufficiently strong, the particulate assemblies go through the so-called jamming transition, during which the number of contacts of a typical particle increases dramatically, and the system becomes rigid. This process of jamming is associated with the development of mesoscale structures, large compared to particle size, and small compared to the size of the system. As a part of this Capstone project, these structures have been studied using a number of tools resulting from percolation theory, statistical mechanics as well as recently developed topological techniques. By combining the results obtained using a variety of different techniques, the participating students have been able to fully describe and quantify the emerging mesoscale structures. The project has continued into a summer research project for one of the participating students, Angelo Taranto. The instructor acknowledges useful input by the collaborating group from Rutgers University, let by Prof. K. Mischaikow. Partial support by NSF grant No. DMS - 1521717 and DARPA contract HR0011-16-2-0033 is also acknowledged.

Diffusion Limited Aggregation

This project, continuation of the project titled `Diffusion Limited Aggregation and Saffman-Taylor Instability in Non-Newtonian Hele-Shaw Flow' focused on formulating and carrying out large scale Monte Carlo simulations that were orders of magnitude more efficient compared to the ones previously developed. As an outcome, these simulations could be carried out with 10s of millions of random walkers, allowing to obtain statistically meaningful results. In addition, an interactive java-based computational tool has been developed, allowing to carry extensive statistical analysis of the obtained results.

Diffusion Limited Aggregation and Saffman-Taylor Instability in Non-Newtonian Hele-Shaw Flow

Two-phase flow in quasi 2D geometry is relevant to a number of applications, in particular related to the flow in porous media. This relevance serves as one important motivation for considering fluid instabillities in the so-called Hele-Shaw geometry (flow between two glass plates). The participating students have carried out experimental, theoretical, and computational study of flow stability in such geometry, focusing in particular on the setup where a less viscous fluid is injected into a more viscous one, in a setup known to lead to instability carrying the name of Saffman-Taylor. The aim of this project has been to study the instability when the more viscous fluid is non-Newtonian, with viscosity that depends on shear rate. To characterize the properties of the emerging patterns, the students have used several methods to calculate the fractal dimension based on the data collected from experimental trials and extensive simulations of diffusion limited aggregation type. Both experimental and computational results suggest that the fractal dimensions between Newtonian and non-Newtonian setups differ. This results, if confirmed, will be of relevance to further work in this field.

Nonlinear waves in coupled pendulum chains

The goal of this project was to observe and understand oscillating patterns in a large array of pendulums. This system provides a simple experimental model in which solitons, or something much like them, can be observed. This system was first studied in the Ph.D. dissertation of Denardo and in several followup articles, from whom some of our images are borrowed. Prof. Goodman learned about this experimental system in a talk by Victor Sanchez-Morcillo at the LENCOS 2012 conference.

Topology and Percolation of Particulate Systems

This project concentrated on the force networks that form as a system of photoelastic particles is compressed. Photoelasticity allows to visualize these force networks and to analyze them using a variety of techniques. In the project, the students carried out physical experiments and produced sets of images (an example is shown). The brightness of a given particle is at least approximately proportional to the total stress exerted. These images were then processed using image processing techniques to extract the information such as size, position, and stress of each particle.

Instabilities of Liquid Crystals

This project explored instabilities occurring during spreading of liquid crystals on solid surfaces and consisted of experimental, computational, and modeling component. The experimental group carried table top experiments with 5CB liquid crystal in nematic phase spreading on horizontal and inclined substrates, with the idea of exploring the influence of complex liquid crystal rheology on the spreading behavior. The figure shows an example of intricate patterns that were observed.

The Shape of a Soap Film in an Electric Field

The project combined analysis and computation with modeling and simple experiments to see how an electrostatic field can alter the shape of a soap film or fluid membrane. Some appreciation that objects can experience a force when placed in an electrostatic field was around before 1752 when Benjamin Franklin used the idea in the invention of "Franklin's Bells". Various types of electroscope were invented soon after. A more quantitative understanding of how an electrostatic field can deform continuous media must have waited for formulation of the Maxwell stress tensor. Our project draws on studies by G.I. Taylor during the 1960's on liquid drops coalescing or breaking up in an electric field (cf. drops in a rain cloud) and the "Taylor cone", which is related to experiments by Zeleny (1917) on electrohydrodynamic "jetting". More recently, electrohydrodynamics has become a topic of interest for the control of a fluid, or of drops and bubbles, in small-scale microfluidic devices, and in solid-phase MEMS that have a variety of applications.

Topology and Granular Materials

This project explored the use of computational homology in understanding structure formation in dense granular materials. Experimental, theoretical, modeling, and computational components were implemented. The experimental group set up and carried out table-top experiments with photo-elastic cylindrical particles and explored their response to applied pressure. Main effort of the computational group consisted of analyzing the images using computational homology and in particular extracting the quantities describing their topological properties. In addition to the experimental images, this group has analyzed the results of molecular dynamics simulations images, such as the one shown in the Figure. This project was supported by NSF Grants NO. DMS-0511514 and 0835611 (PI: Kondic).

Belousov-Zhabotinsky (BZ) Reaction

Oscillating chemical reaction is thought to be the key to many regulatory processes in living cells, such as the mechanisms that turn on and off the enzymes that transcribe DNA or the contraction of a muscle. The BZ reaction has been the subject of on-going research in chemistry, dynamical systems, and math biology. Our project is to quantify the chemical oscillation in the well-stirred BZ reaction, and visualize the pattern formation due to the instability of traveling chemical fronts in the non-stirred BZ reaction. Experimentally we follow several recipes for the well-stirred BZ reaction, each group of students has their own. For the non-stirred BZ reaction we use the package from "Science Kit and Boreal Laboratories".

Instability of a Fluid Strip

Waves on the surface of a thin liquid film have intrigued researchers for several years. Numerous experimental and modeling studies have been reported. Due to the presence of the free surface, governing non-linear Navier-Stokes(N-S) equations are considerably difficult to analyze. Thus effort was made to describe these surface waves using low-dimensional models derived from the N-S equations. Our project is composed of three parts. Experimentally we use a goniometer to record the profile of a strip flowing down an inclined and inverted surfaces, using two types of solids. Computationally, we solve the PDE for the fluid height for the two types of solids. Theoretically, we discuss the similarities and differences between the waves observed on falling films, and the ones present in the case of the flow down an inverted surface.

Shape and Break-up of a Pendant Drop

A liquid drop forms a distinct shape as it hangs or breaks up.In the case of a pendant (hanging) drop, its shape is described by a system of ordinary differential equations which define a boundary value problem. Using Runge-Kutta numerical algorithm, we solve these equations. A comparison of the results with the experimental drop shapes, obtained using a goniometer, is then carried out. In addition, we extend our computations in order to calculate surface tension of a pendant drop by minimizing the difference between computed and measured drop shapes (pendant drop method for determining surface tension). Finally, we report the results of the experiments of a drop break-up carried out using a high speed camera. These results are used to analyze the breakup process and compare the experimental results to a self-similar solution.

Simulations and Experiments with Evaporative Drops

This project presents theoretical, computational, and experimental aspects of mass-loss of fluid drops due to evaporation. The theoretical component consists of using basic principles such as conservation of mass, momentum, and energy together with an evaporation model to derive an evolution equation for a fluid drop. This equation is solved and analyzed for comparison with the experimental results for fluids such as water, 70% and 100% isopropyl alcohol. Experiments were performed using a professional grade goniometer which allowed us to precisely measure contact angle and volume as a function of time. The comparison between computational results and experimental results is focused on the change in volume, mass, and contact angle. In addition, we show curious instabilities which developed for 100% isopropyl alcohol drops.

Classical Mechanics and Rigid Body Motions

In a recent SIAM Review article, Diaconis, Holmes, and Montgomery have shown that under general conditions, a coin is inherently biased to land heads-up if it leaves the hand heads-up. This effect does not diminish as the coin is thrown higher or with more vigorous rotation and is not due to any asymmetry in the minted coin. This bias arises because the coin precesses as it tumbles, and is a straightforward, though novel, application of results due to Euler in about 1750. This result formed the culminating experiment of a capstone course in applied mathematics at NJIT. The first few weeks of the course were spent teaching the relevant results from classical mechanics. Several experiments were conducted using Capstone Laboratory equipment, ordinary digital cameras, and software from the Matlab Image Processing toolbox.

The Belousov-Zhabotinsky Chemical Reaction

This semester the course considered the BZ reaction in a closed reactor (glass beaker) with continuous stirring (spatially homogeneous reaction). We performed the experiment and modeled it with a system of ordinary differential equations. First, the students learned how to use the Law of Mass Action to derive ordinary differential equation models of chemical reactions. Then, nonlinear-dynamics theoretical tools for the analysis of the resulting finite-dimensional dynamical system of ordinary differential equations were employed to analytically study the resulting models. Also, the students employed potentiometric methods to directly measure the concentrations of the important components in this reaction using special electrodes and the LabPro equipment; the experimental results were compared to the theoretical model result.

Ripple tank Demonstrations of Linear Wave Phenomena

The main purpose of the project was to analyze and demonstrate diffraction - loosely, the ability of a wave to `slightly bend around a corner' or other sharp edge in its path, or - for light - to blur the light-dark boundary at the edge of a shadow.

Hele-Shaw Flow Past Obstacles

In this project, students used the Hele-Shaw apparatus to perform experiments of flow around a cylinder and flow around an airfoil at various angles of attack. The experimental data was then analyzed and compared with theoretical predictions. Theoretical results were obtained by first reducing the full, three-dimensional Navier-Stokes equations to the appropriate 2D form using the basic physics of the problem and scaling arguments.

Flow of Thin Films

The experimental part of this project has been performed using previously build platform consisting of a frame covered by a sheet of glass. The fluid is then released to flow under gravity down a plane. Very quickly the fluid front (contact line) becomes unstable and develops patterns. The figure shows the resulting pattern for the flow of partially wetting fluid (glycerol) down an `inverted' plane characterized by an inclination angle of 120 degrees relative to horizontal. The students used small amount of food coloring and in addition image processing to reach high contrast allowing for good visualization.

Hele-Shaw flow past obstacles

This project used Hele-Shaw setup to analyze flow around obstacles in highly controlled environment. The performed experiments included flow around a cylinder, flow around a blunt body, and flow around an airfoil under different angles of attack. The figure shows an example of this flow, where the streamlines of the flow are visualized using ink sources distributed at the entrance to the flow domain (left hand side of the figure).

Instabilities of two-fluid flow in Hele-Shaw geometry

When a low viscosity fluid (for example, water) is injected into a more viscous one, such as glycerin, an instability occurs. The figure shows an example of this instability (often called Saffman-Taylor instability) in the Hele-Shaw geometry, where blue water is injected into a colorless glycerin. One important reason for studying this problem is that it is closely related to many technologically relevant ones, such as flow in porous media.

Pattern formation in thin liquid film flows

When a thin viscous film is released, the fluid front becomes unstable and develop finger-like patterns. Such instability is relevant in a number of important technological processes and has been extensively explored experimentally, computationally, and theoretically. In this project, the participating students built the apparatus to explore the instability mechanism, and have carried out linear stability analysis allowing to develop a basic understanding of instability development.