Complex Flows and Soft Matter Group

Biofluids

Our research in biofluids focuses mainly on applications arising in tissue engineering. A common experimental protocol in tissue engineering involves seeding cells (e.g. osteocytes or chondrocytes) onto a porous biodegradable scaffold, which can then be placed into a chamber (a "bioreactor") and perfused with nutrient-rich culture medium. The nutrient, together with the shear stress imparted by the flow to the cell surface, stimulates cell proliferation.

We propose and solve mathematical models describing the growth of tissue within such porous scaffolds. Recent work (described in the publications below) has focused on how the scaffold can be manipulated, both chemically and mechanically, in order to provide improved net tissue yield. Current work is concerned with tissue growth within individual scaffold pores, in particular, how the internal pore geometry can affect the final tissue distribution and total yield.

Another current project concerns mathematical modeling of Ischemia-Reperfusion Injury (IRI), the paradoxical further injury that can result to tissue when blood flow is restored after a period of ischemia. A complicated sequence of biochemical reactions, triggered by the reintroduction of shear stress at the endothelial wall when flow is restored, and by the reintroduction of oxygen, can lead to the production of Reactive Oxygen Species (ROS) which can cause cell damage and possibly death. We are studying the potential of so-called "postconditioning therapy", in which the blood flow is restored gradually, rather than abruptly, to the ischemic organ. Our model investigates the efficacy of various postconditioning therapies in an attempt to determine optimal (injury minimizing) scenarios.

Recent Publications



P. Sanaei, L. J. Cummings, S. L. Waters, and I. M. Griffiths, Curvature- and fluid-stress-driven tissue growth in a tissue-engineering scaffold pore, Biomechanics and Modeling in Mechanobiology, 18(3), 589-605, (2018)





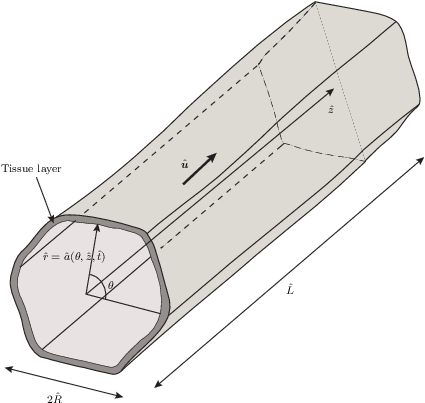
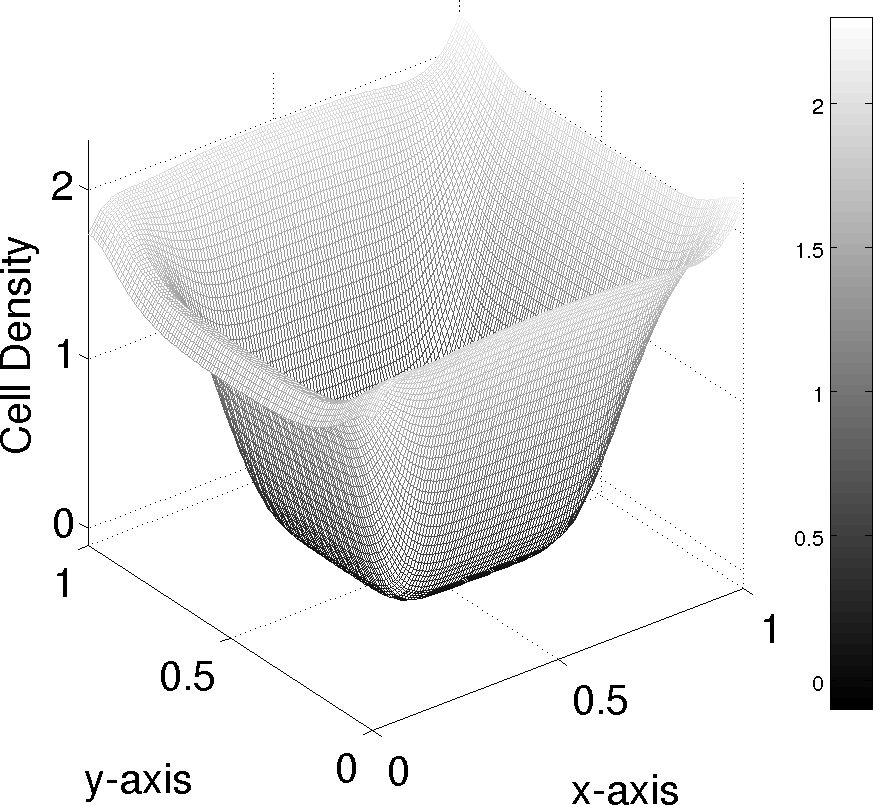
Cell proliferation within a fluid-filled porous tissue-engineering scaffold depends on a sensitive choice of pore geometry and flow rates: regions of high curvature encourage cell proliferation, while a critical flow rate is required to promote growth for certain cell types. When the flow rate is too slow, the nutrient supply is limited; when it is too fast, cells may be damaged by the high fluid shear stress. As a result, determining appropriate tissue-engineering-construct geometries and operating regimes poses a significant challenge that cannot be addressed by experimentation alone. In this paper, we present a mathematical theory for the fluid flow within a pore of a tissue-engineering scaffold, which is coupled to the growth of cells on the pore walls. We exploit the slenderness of a pore that is typical in such a scenario, to derive a reduced model that enables a comprehensive analysis of the system to be performed. We derive analytical solutions in a particular case of a nearly piecewise constant growth law and compare these with numerical solutions of the reduced model. Qualitative comparisons of tissue morphologies predicted by our model, with those observed experimentally, are also made. We demonstrate how the simplified system may be used to make predictions on the design of a tissue-engineering scaffold and the appropriate operating regime that ensures a desired level of tissue growth.

J.V. Pohlmeyer, S.L. Waters, and L.J. Cummings, Mathematical model of growth factor driven haptotaxis and proliferation in a tissue engineering scaffold, Bulletin of mathematical biology, 75, 393-427, (2013)





Motivated by experimental work (Miller et al. in Biomaterials 27(10):2213 –2221, 2006, 32(11):2775–2785, 2011) we investigate the effect of growth factor driven haptotaxis and proliferation in a perfusion tissue engineering bioreactor, in which nutrient-rich culture medium is perfused through a 2D porous scaffold impregnated with growth factor and seeded with cells. We model these processes on the timescale of cell proliferation, which typically is of the order of days. While a quantitative representation of these phenomena requires more experimental data than is yet available, qualitative agreement with preliminary experimental studies (Miller et al. in Biomaterials 27(10):2213–2221, 2006) is obtained, and appears promising. The ultimate goal of such modeling is to ascertain initial conditions (growth factor distribution, initial cell seeding, etc.) that will lead to a final desired outcome.

Animation

J.V. Pohlmeyer, and L.J. Cummings, Cyclic loading of growing tissue in a bioreactor: mathematical model and asymptotic analysis, Bulletin of mathematical biology, 75, 2450-2473, (2013)





A simplified 2D mathematical model for tissue growth within a cyclicallyloaded tissue engineering scaffold is presented and analyzed. Such cyclic loading has the potential to improve yield and functionality of tissue such as bone and cartilage when grown on a scaffold within a perfusion bioreactor. The cyclic compression affects the flow of the perfused nutrient, leading to flow properties that are inherently unsteady, though periodic, on a timescale short compared with that of tissue proliferation. A two-timescale analysis based on these well-separated timescales is exploited to derive a closed model for the tissue growth on the long timescale of proliferation. Some sample numerical results are given for the final model, and discussed.