Walking Droplets

Recent Publications

J. W. M. Bush and A. U. Oza, Hydrodynamic quantum analogs, Reports on Progress in Physics, 84, 017001, (2020)

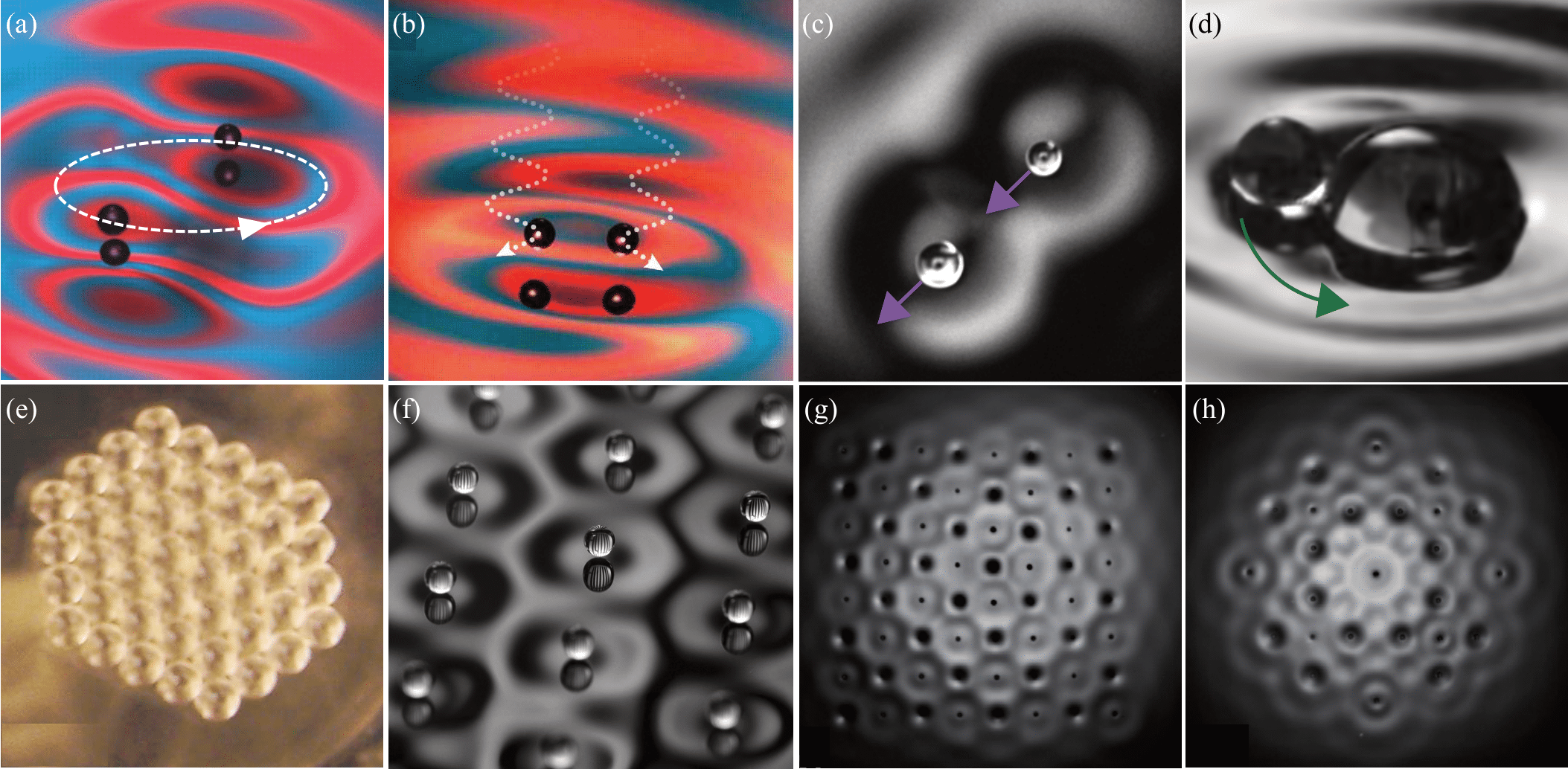
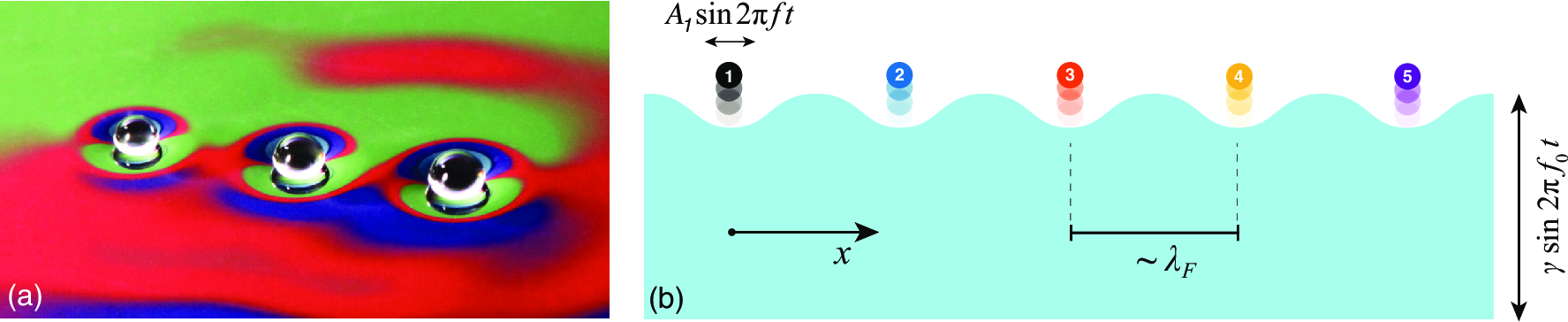
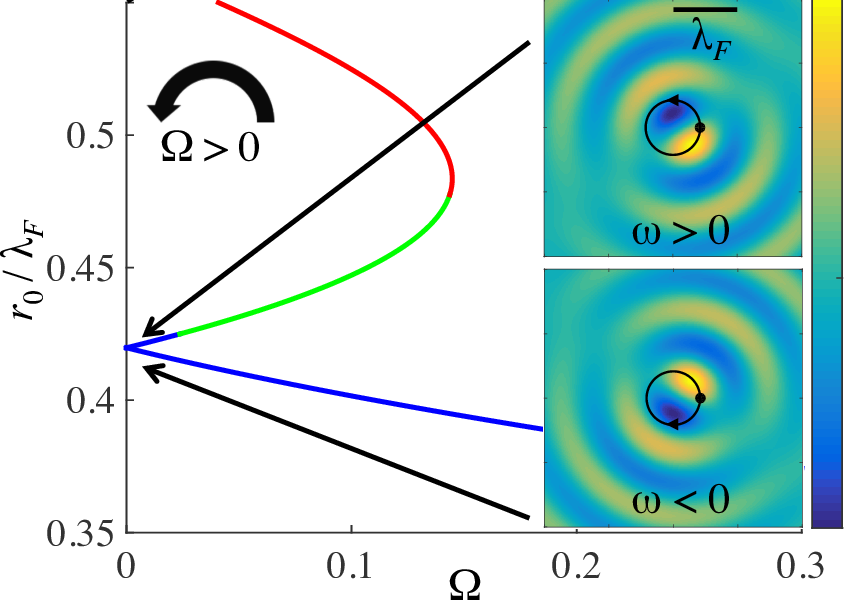
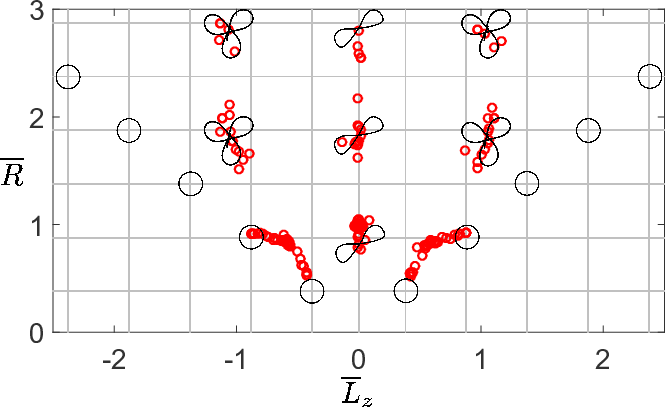
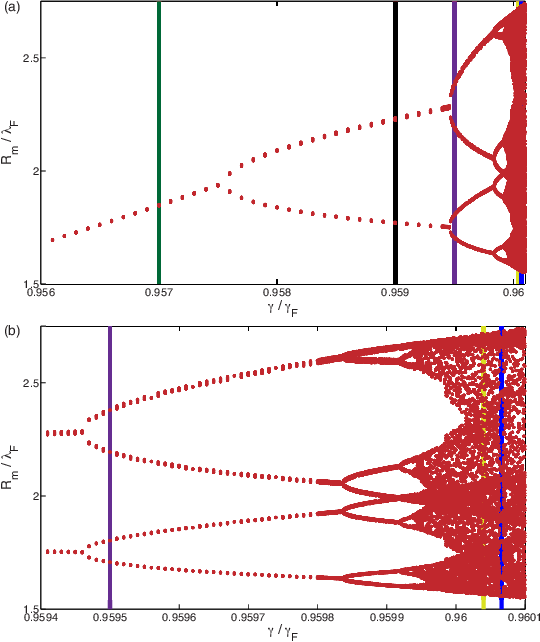
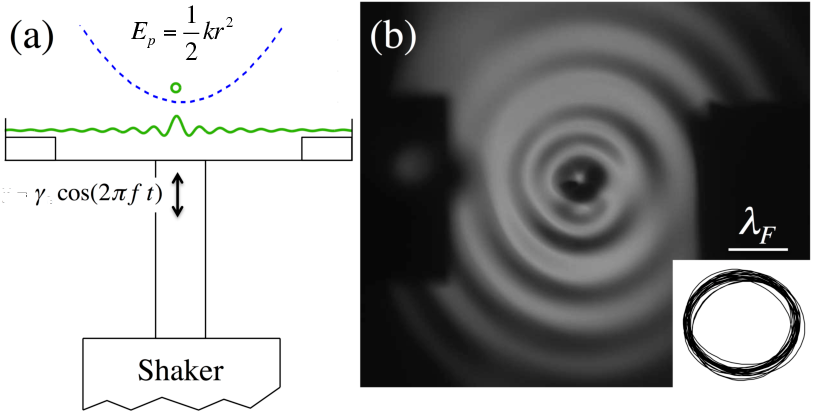
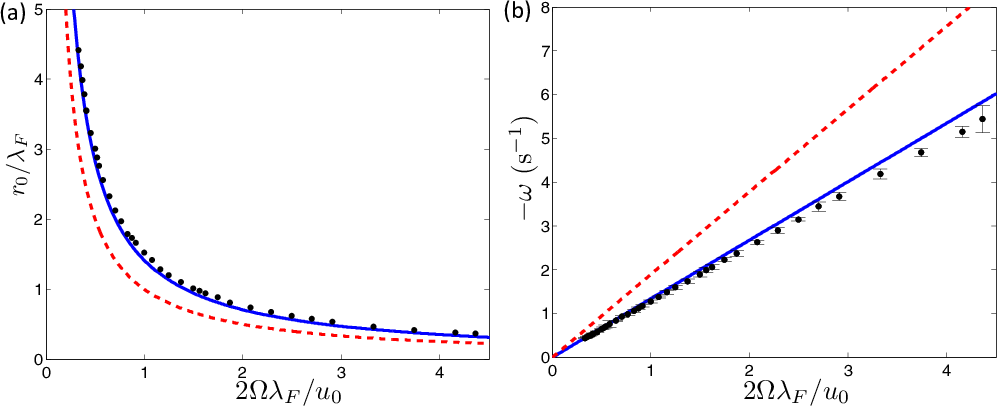
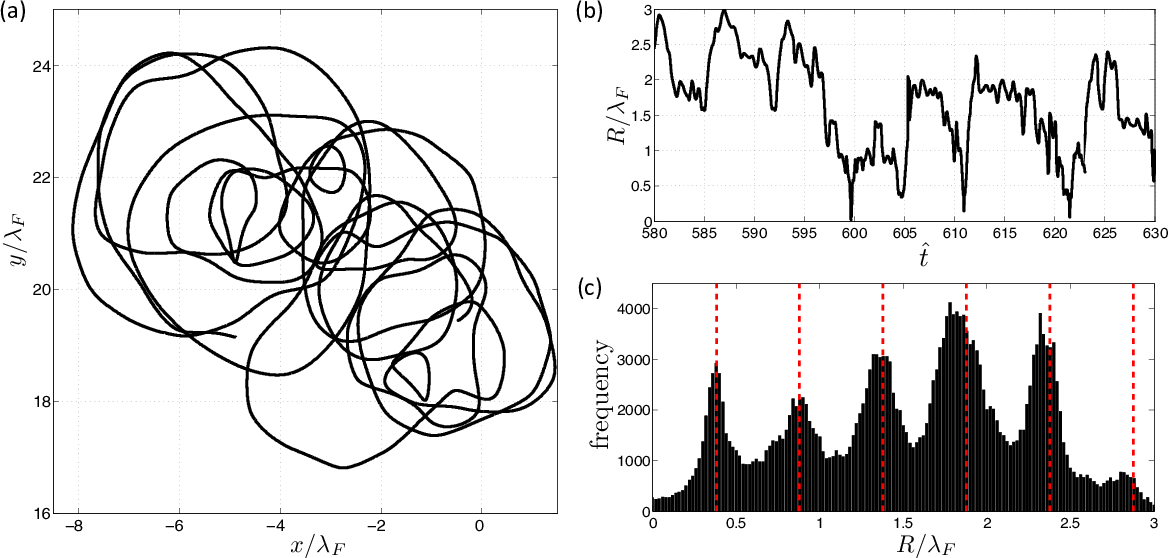
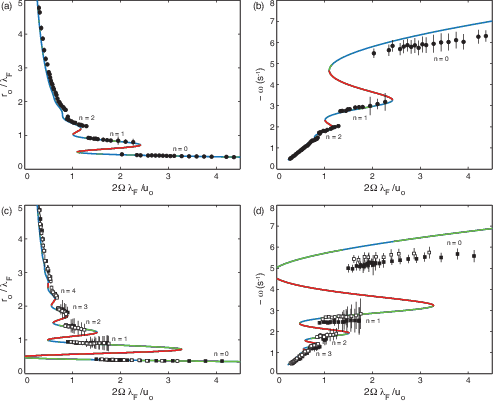
The walking droplet system discovered by Yves Couder and Emmanuel Fort presents an example of a vibrating particle self-propelling through a resonant interaction with its own wave field. It provides a means of visualizing a particle as an excitation of a field, a common notion in quantum field theory. Moreover, it represents the first macroscopic realization of a form of dynamics proposed for quantum particles by Louis de Broglie in the 1920s. The fact that this hydrodynamic pilot-wave system exhibits many features typically associated with the microscopic, quantum realm raises a number of intriguing questions. At a minimum, it extends the range of classical systems to include quantum-like statistics in a number of settings. A more optimistic stance is that it suggests the manner in which quantum mechanics might be completed through a theoretical description of particle trajectories. We here review the experimental studies of the walker system, and the hierarchy of theoretical models developed to rationalize its behavior. Particular attention is given to enumerating the dynamical mechanisms responsible for the emergence of robust, structured statistical behavior. Another focus is demonstrating how the temporal nonlocality of the droplet dynamics, as results from the persistence of its pilot wave field, may give rise to behavior that appears to be spatially nonlocal. Finally, we describe recent explorations of a generalized theoretical framework that provides a mathematical bridge between the hydrodynamic pilot-wave system and various realist models of quantum dynamics.

L. Barnes, G. Pucci, and A. U. Oza, Resonant interactions in bouncing droplet chains, Comptes Rendus. Mécanique, 348, 573--589, (2020)

In a pioneering series of experiments, Yves Couder, Emmanuel Fort and coworkers demonstrated that droplets bouncing on the surface of a vertically vibrating fluid bath exhibit phenomena reminiscent of those observed in the microscopic quantum realm. Inspired by this discovery, we here conduct a theoretical and numerical investigation into the structure and dynamics of one-dimensional chains of bouncing droplets. We demonstrate that such chains undergo an oscillatory instability as the system's wave-induced memory is increased progressively. The predicted oscillation frequency compares well with previously reported experimental data. We then investigate the resonant oscillations excited in the chain when the drop at one end is subjected to periodic forcing in the horizontal direction. At relatively high memory, the drops may oscillate with an amplitude larger than that prescribed, suggesting that the drops effectively extract energy from the collective wave field. We also find that dynamic stabilization of new bouncing states can be achieved by forcing the chain at high frequency. Generally, our work provides insight into the collective behavior of particles interacting through long-range and temporally nonlocal forces.

A. U. Oza, R. R. Rosales, and J. W. M. Bush, Hydrodynamic spin states, Chaos: An Interdisciplinary Journal of Nonlinear Science, 28, 096106, (2018)

We present the results of a theoretical investigation of hydrodynamic spin states, wherein a droplet walking on a vertically vibrating fluid bath executes orbital motion despite the absence of an applied external field. In this regime, the walker’s self-generated wave force is sufficiently strong to confine the walker to a circular orbit. We use an integro-differential trajectory equation for the droplet’s horizontal motion to specify the parameter regimes for which the innermost spin state can be stabilized. Stable spin states are shown to exhibit an analog of the Zeeman effect fromd quantum mechanics when they are placed in a rotating frame.

Arbelaiz, Juncal; Oza, Anand U.; and Bush, John W. M., Promenading pairs of walking droplets: Dynamics and stability, Phys. Rev. Fluids, 3, 013604, (2018)

We present the results of an integrated experimental and theoretical investigation of the promenade mode, a bound state formed by a pair of droplets walking side by side on the surface of a vibrating fluid bath. Particular attention is given to characterizing the dependence of the promenading behavior on the vibrational forcing for drops of a given size. We also enumerate the different instabilities that may arise, including transitions to smaller promenade modes or orbiting pairs. Our theoretical developments highlight the importance of the vertical bouncing dynamics on the stability characteristics. Specifically, quantitative comparison between experiment and theory prompts further refinement of the stroboscopic model [A. U. Oza et al., J. Fluid Mech. 737, 552 (2013)] through inclusion of phase adaptation and reveals the critical role that impact phase variations play in the stability of the promenading pairs.

Animation

A. U. Oza, E. Siéfert, D. M. Harris, J. Moláček, and J. W. M. Bush, Orbiting pairs of walking droplets: Dynamics and stability, Physical Review Fluids, 2, 053601, (2017)

A decade ago, Couder and Fort [Phys. Rev. Lett. 97, 154101 (2006)] discovered that a millimetric droplet sustained on the surface of a vibrating fluid bath may self-propel through a resonant interaction with its own wave field. We here present the results of a combined experimental and theoretical investigation of the interactions of such walking droplets. Specifically, we delimit experimentally the different regimes for an orbiting pair of identical walkers and extend the theoretical model of Oza et al. [J. Fluid Mech. 737, 552 (2013)] in order to rationalize our observations. A quantitative comparison between experiment and theory highlights the importance of spatial damping of the wave field. Our results also indicate that walkers adapt their impact phase according to the local wave height, an effect that stabilizes orbiting bound states.

Animation

K. M. Kurianski, A. U. Oza, and J. W. M. Bush,, Simulations of pilot-wave dynamics in a simple harmonic potential, Physical Review Fluids, 2, 113602, (2017)

We present the results of a numerical investigation of droplets walking in a harmonic potential on a vibrating fluid bath. The droplet's trajectory is described by an integro-differential equation, which is simulated numerically in various parameter regimes. We produce a regime diagram that summarizes the dependence of the walker's behavior on the system parameters for a droplet of fixed size. At relatively low vibrational forcing, a number of periodic and quasiperiodic trajectories emerge. In the limit of large vibrational forcing, the walker's trajectory becomes chaotic, but the resulting trajectories can be decomposed into portions of unstable quasiperiodic states.

L. D. Tambasco, D. M. Harris, A. U. Oza, R. R. Rosales, and J. W. M. Bush, The onset of chaos in orbital pilot-wave dynamics, Chaos: An Interdisciplinary Journal of Nonlinear Science, 26, 103107, (2016)

We present the results of a numerical investigation of the emergence of chaos in the orbital dynamics of droplets walking on a vertically vibrating fluid bath and acted upon by one of the three different external forces, specifically, Coriolis, Coulomb, or linear spring forces. As the vibrational forcing of the bath is increased progressively, circular orbits destabilize into wobbling orbits and eventually chaotic trajectories. We demonstrate that the route to chaos depends on the form of the external force. When acted upon by Coriolis or Coulomb forces, the droplet's orbital motion becomes chaotic through a period-doubling cascade. In the presence of a central harmonic potential, the transition to chaos follows a path reminiscent of the Ruelle-Takens-Newhouse scenario.

M. Labousse, A. U. Oza, S. Perrard, and J.W. M. Bush, Pilot-wave dynamics in a harmonic potential: Quantization and stability of circular orbits, Physical Review E, 93, 033122, (2016)

We present the results of a theoretical investigation of the dynamics of a droplet walking on a vibrating fluid bath under the influence of a harmonic potential. The walking droplet's horizontal motion is described by an integro-differential trajectory equation, which is found to admit steady orbital solutions. Predictions for the dependence of the orbital radius and frequency on the strength of the radial harmonic force field agree favorably with experimental data. The orbital quantization is rationalized through an analysis of the orbital solutions. The predicted dependence of the orbital stability on system parameters is compared with experimental data and the limitations of the model are discussed.

J.W. M. Bush, A. U. Oza, and J. Moláček, The wave-induced added mass of walking droplets, Journal of Fluid Mechanics, 755, R7, (2014)

It has recently been demonstrated that droplets walking on a vibrating fluid bath exhibit several features previously thought to be peculiar to the microscopic realm. The walker, consisting of a droplet plus its guiding wavefield, is a spatially extended object. We here examine the dependence of the walker mass and momentum on its velocity. Doing so indicates that, when the walker's time scale of acceleration is long relative to the wave decay time, its dynamics may be described in terms of the mechanics of a particle with a speed-dependent mass and a nonlinear drag force that drives it towards a fixed speed. Drawing an analogy with relativistic mechanics, we define a hydrodynamic boost factor for the walkers. This perspective provides a new rationale for the anomalous orbital radii reported in recent studies.

A. U. Oza, Ø. Wind-Willassen, D. M. Harris, R. R. Rosales, and J. W. M. Bush, Pilot-wave hydrodynamics in a rotating frame: Exotic orbits, Physics of Fluids, 26, 082101, (2014)

We present the results of a numerical investigation of droplets walking on a rotating vibrating fluid bath. The drop's trajectory is described by an integro-differential equation, which is simulated numerically in various parameter regimes. As the forcing acceleration is progressively increased, stable circular orbits give way to wobbling orbits, which are succeeded in turn by instabilities of the orbital center characterized by steady drifting then discrete leaping. In the limit of large vibrational forcing, the walker's trajectory becomes chaotic, but its statistical behavior reflects the influence of the unstable orbital solutions. The study results in a complete regime diagram that summarizes the dependence of the walker's behavior on the system parameters. Our predictions compare favorably to the experimental observations of Harris and Bush (“Droplets walking in a rotating frame: from quantized orbits to multi- modal statistics,” J. Fluid Mech. 739, 444–464 (2014)).

A. U. Oza, D. M. Harris, R. R. Rosales, and J. W. M. Bush, Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization, Journal of Fluid Mechanics, 744, 404-429, (2014)

We present the results of a theoretical investigation of droplets walking on a rotating vibrating fluid bath. The droplet's trajectory is described in terms of an integro-differential equation that incorporates the influence of its propulsive wave force. Predictions for the dependence of the orbital radius on the bath's rotation rate compare favourably with experimental data and capture the progression from continuous to quantized orbits as the vibrational acceleration is increased. The orbital quantization is rationalized by assessing the stability of the orbital solutions, and may be understood as resulting directly from the dynamic constraint imposed on the drop by its monochromatic guiding wave. The stability analysis also predicts the existence of wobbling orbital states reported in recent experiments, and the absence of stable orbits in the limit of large vibrational forcing.

A. U. Oza, R. R. Rosales, and J. W. M. Bush, A trajectory equation for walking droplets: hydrodynamic pilot-wave theory, Journal of Fluid Mechanics, 737, 552-570, (2013)

We present the results of a theoretical investigation of droplets bouncing on a vertically vibrating fluid bath. An integro-differential equation describing the horizontal motion of the drop is developed by approximating the drop as a continuous moving source of standing waves. Our model indicates that, as the forcing acceleration is increased, the bouncing state destabilizes into steady horizontal motion along a straight line, a walking state, via a supercritical pitchfork bifurcation. Predictions for the dependence of the walking threshold and drop speed on the system parameters compare favourably with experimental data. By considering the stability of the walking state, we show that the drop is stable to perturbations in the direction of motion and neutrally stable to lateral perturbations. This result lends insight into the possibility of chaotic dynamics emerging when droplets walk in complex geometries.