Granular Matter

Recent Publications

L. Kovalcinova, A. Taranto, and L. Kondic, Properties of interaction networks in compressed two and three dimensional particulate systems, Granu. Matter, 26, 1-15, (2024)

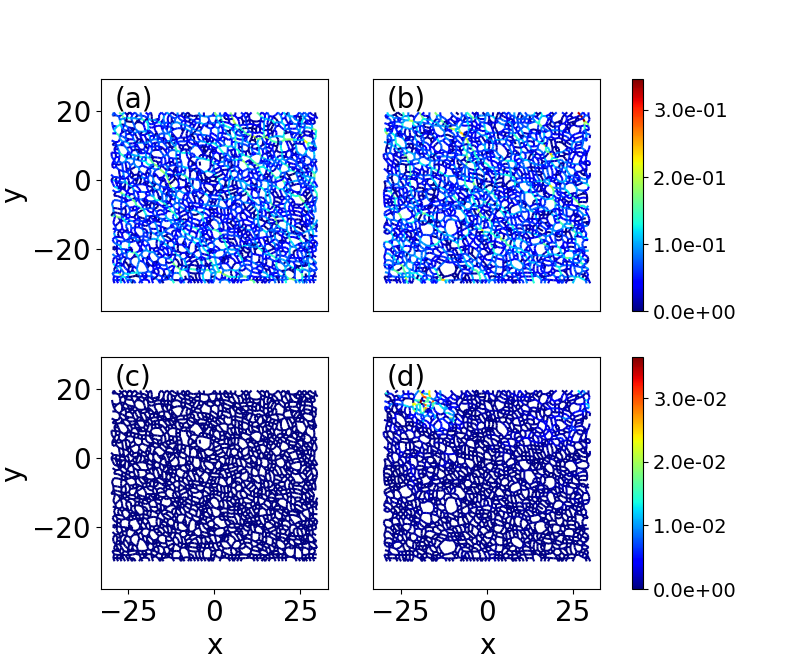
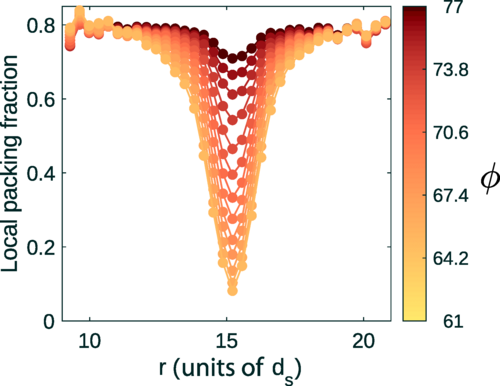
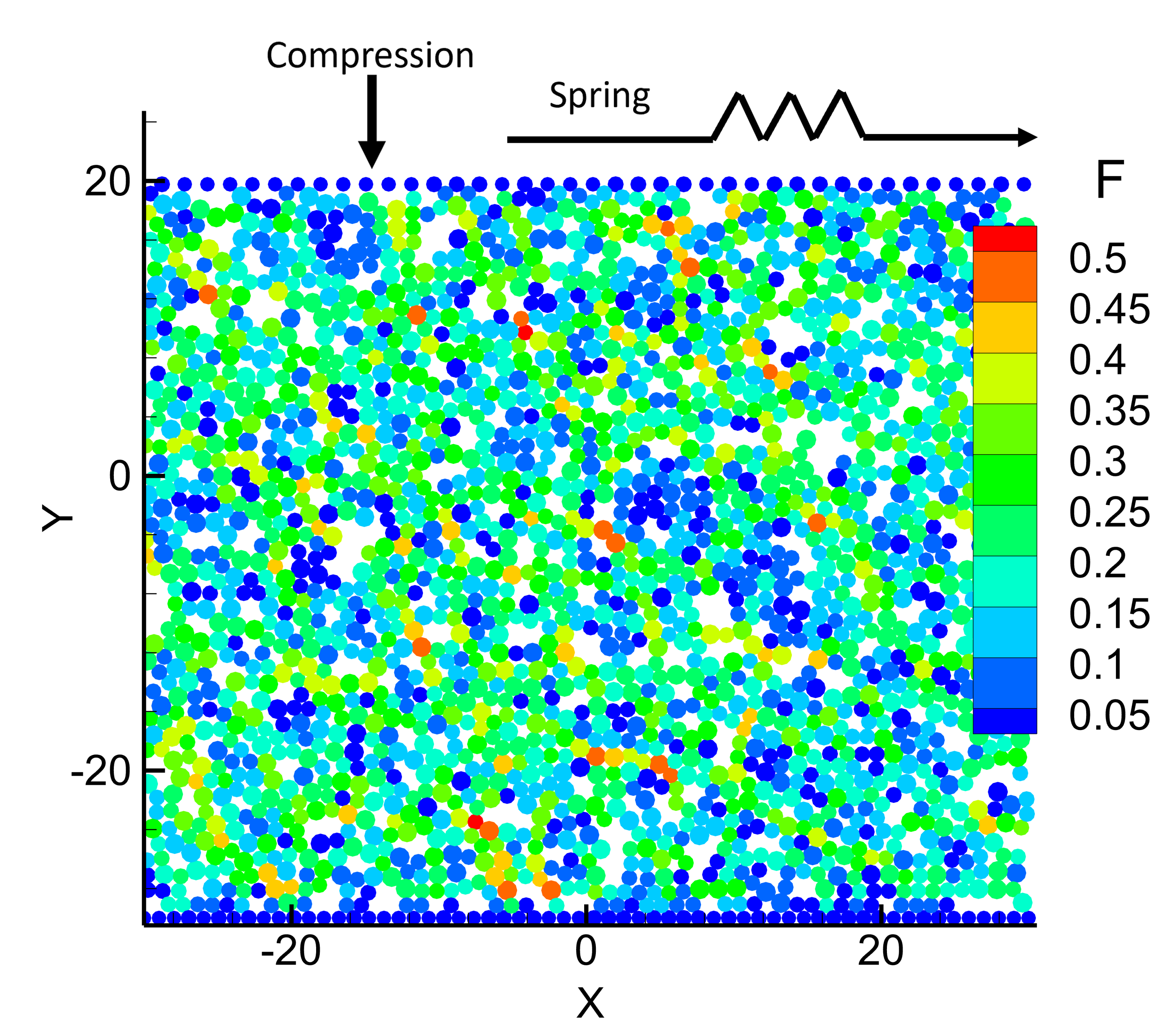
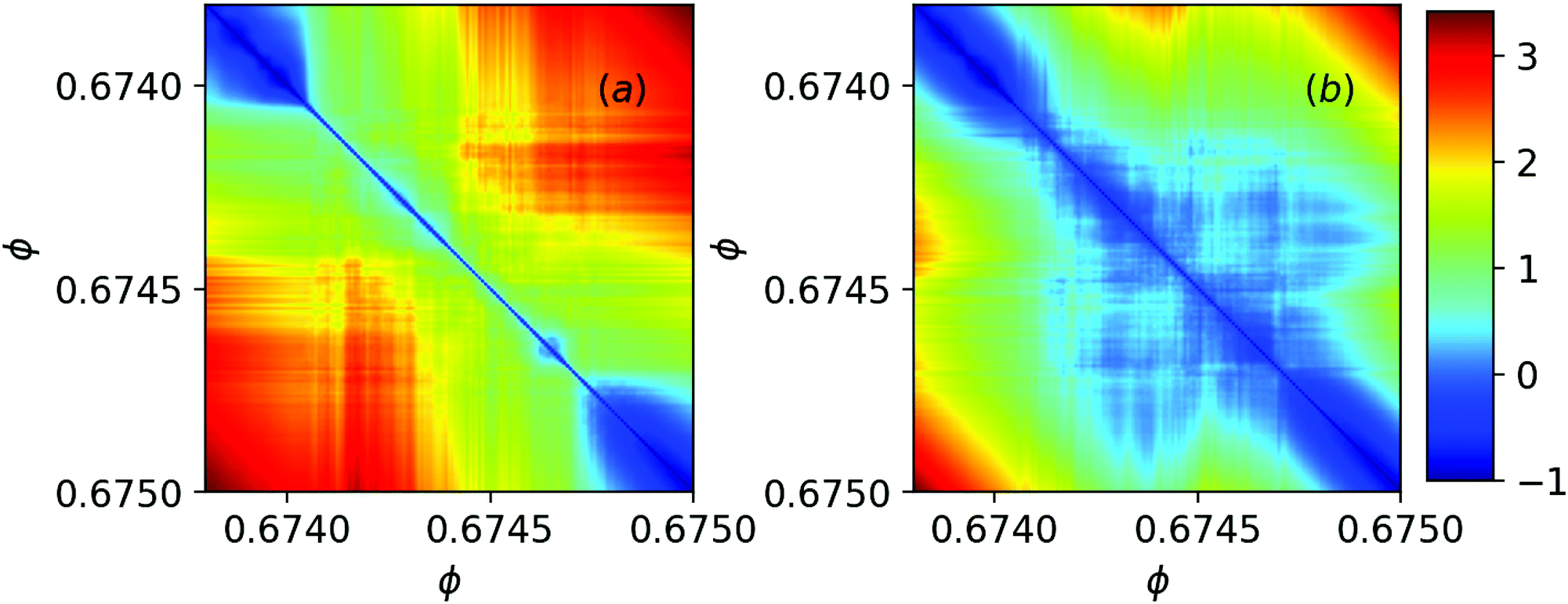
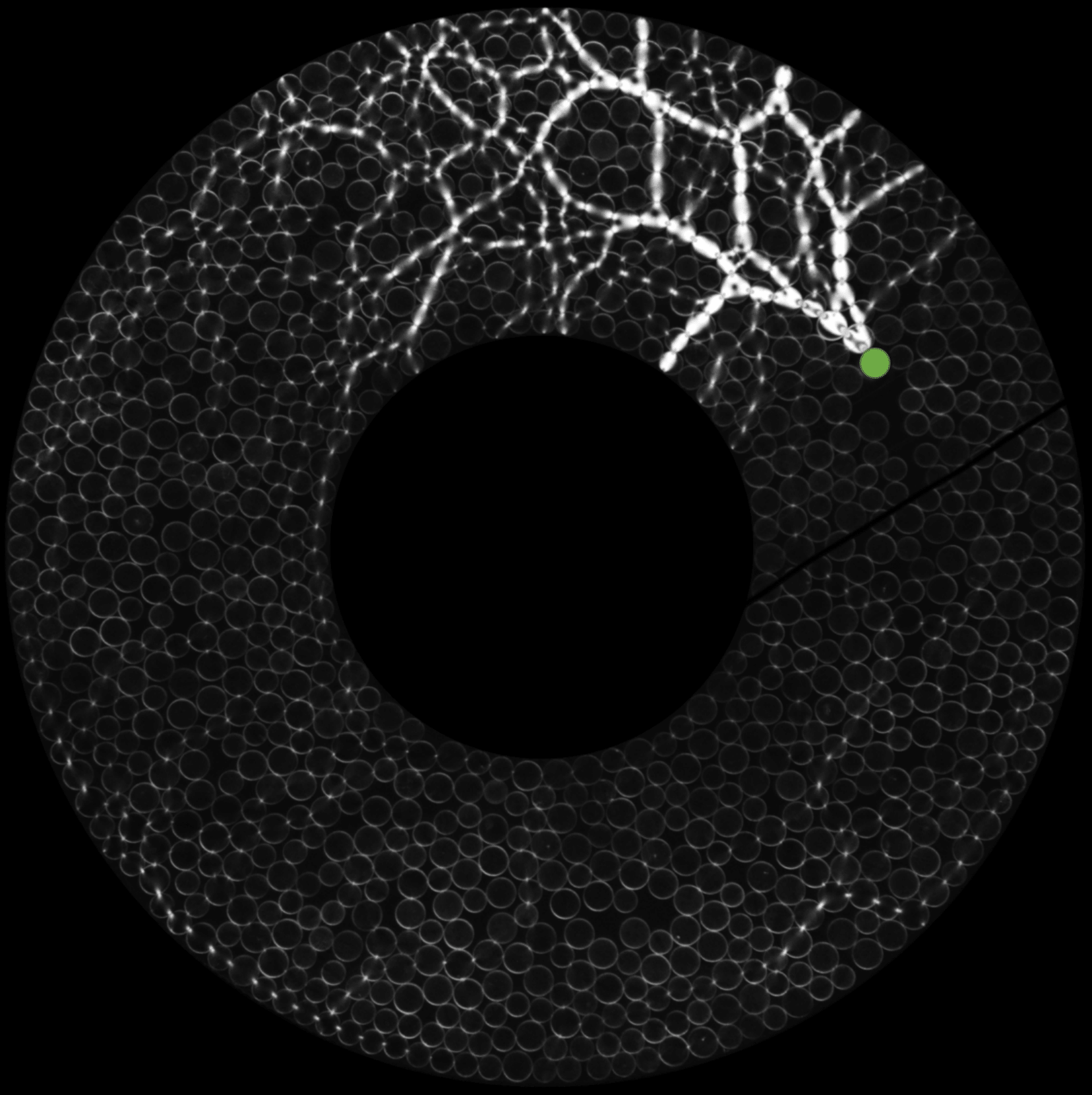
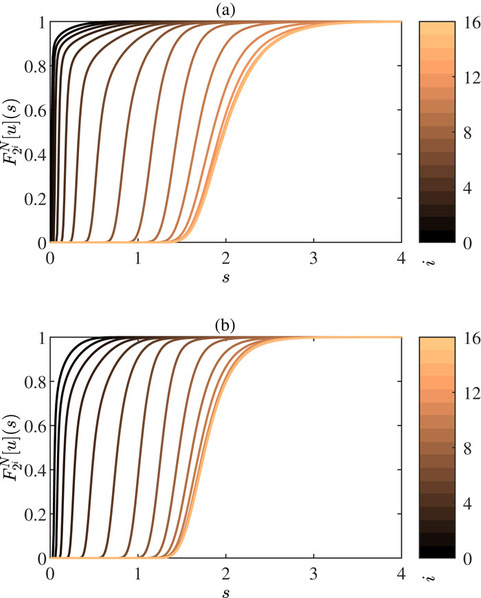
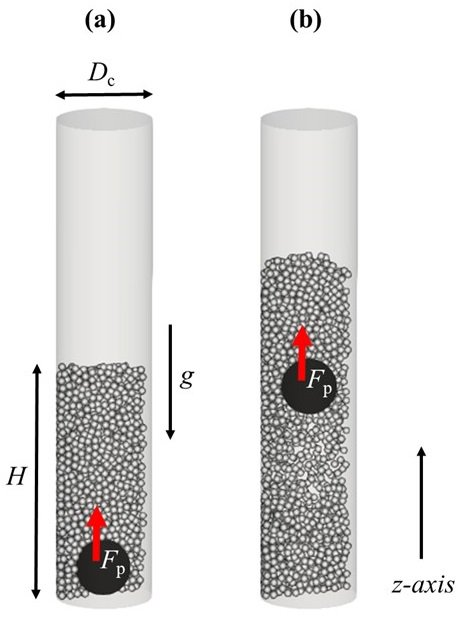
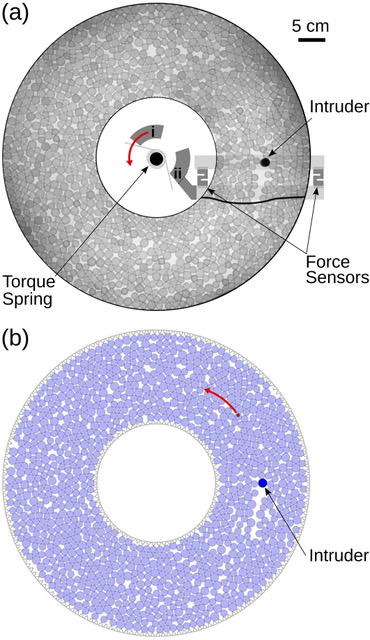
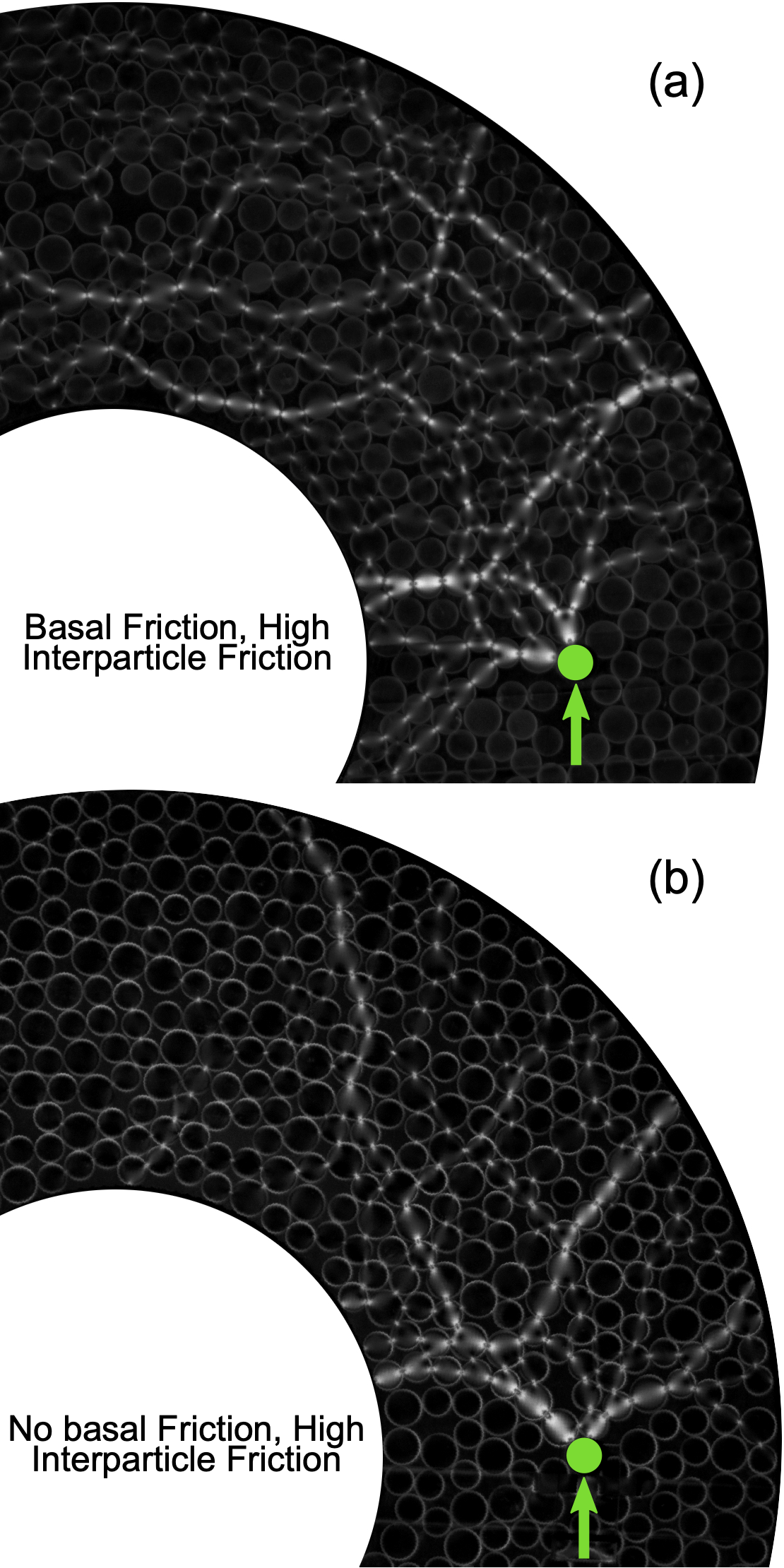
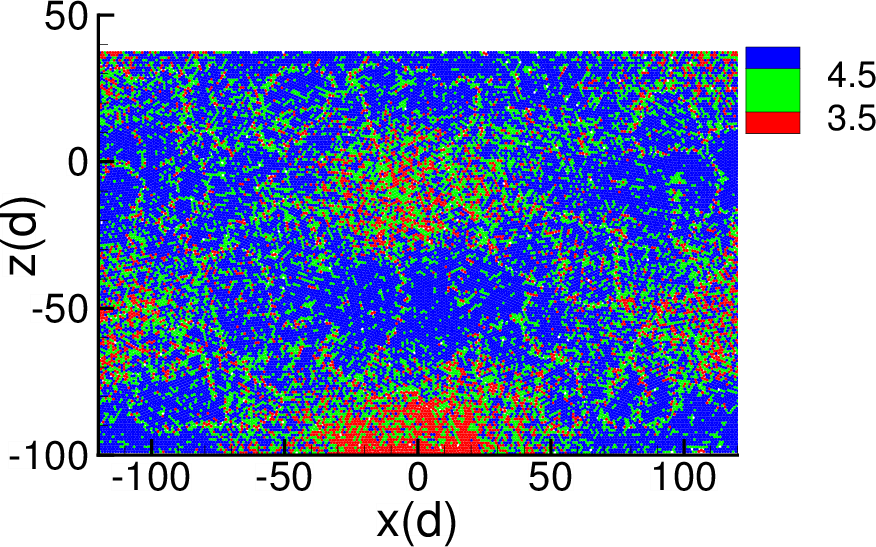
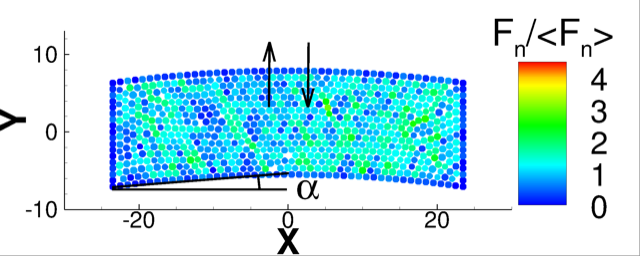
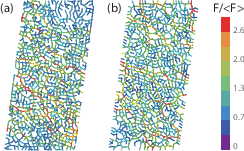
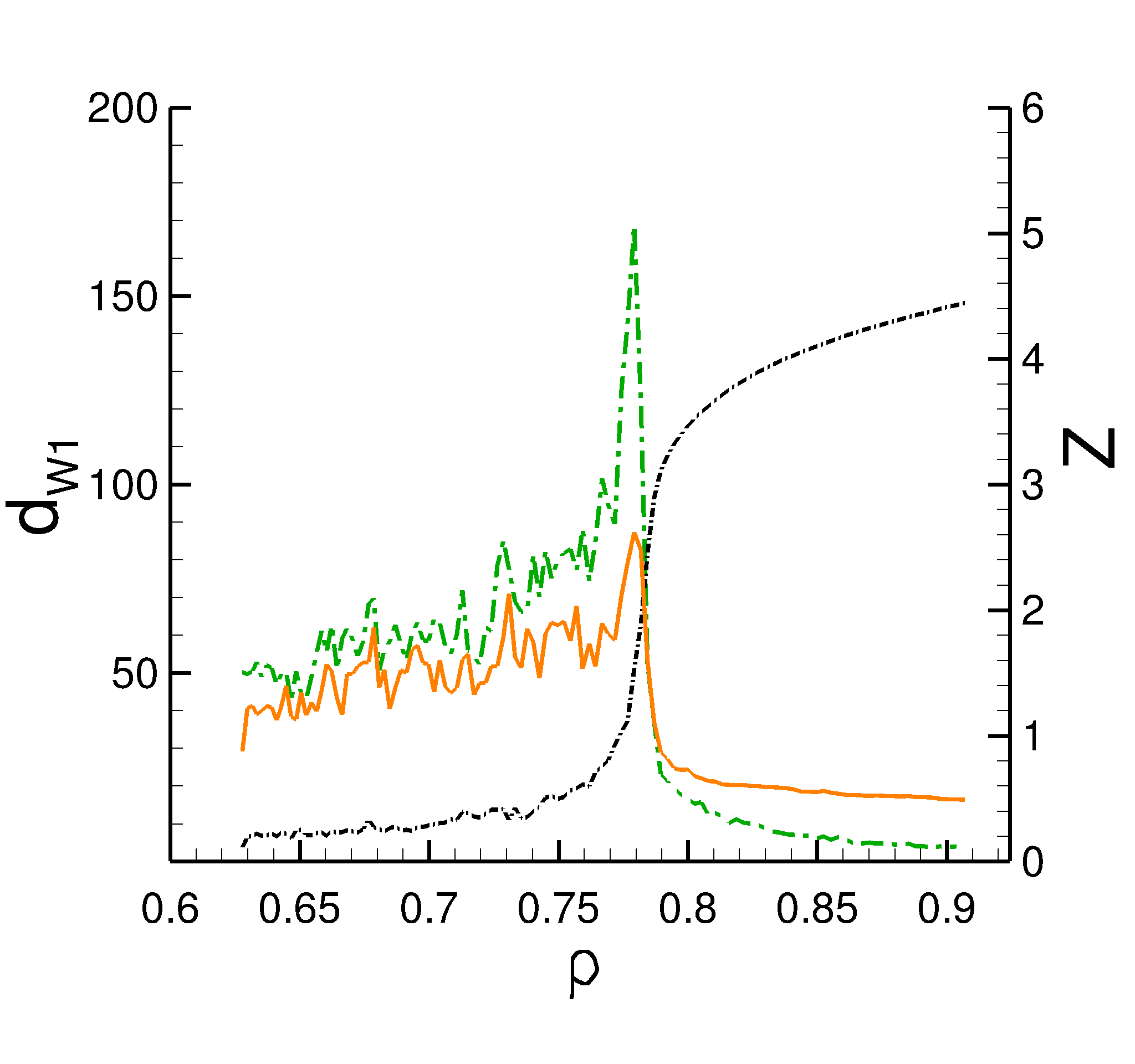
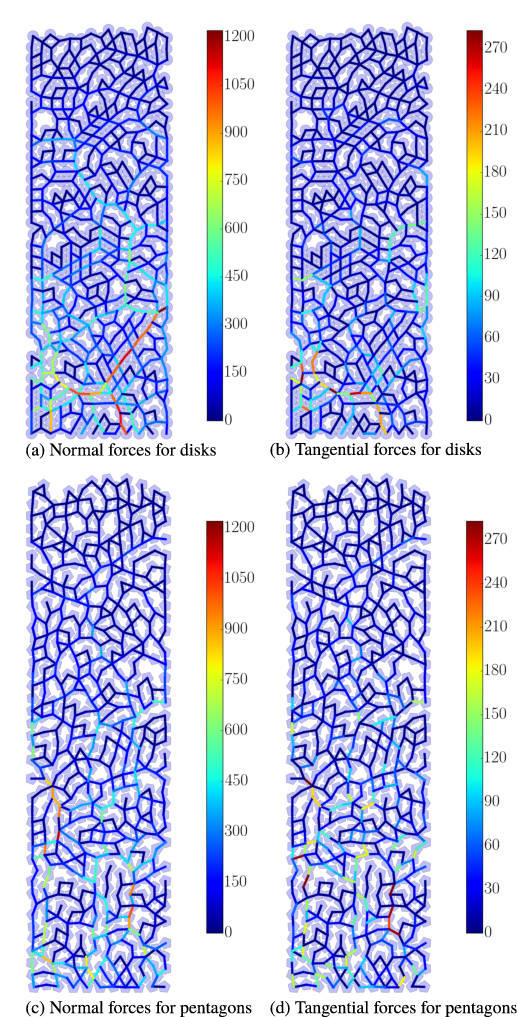
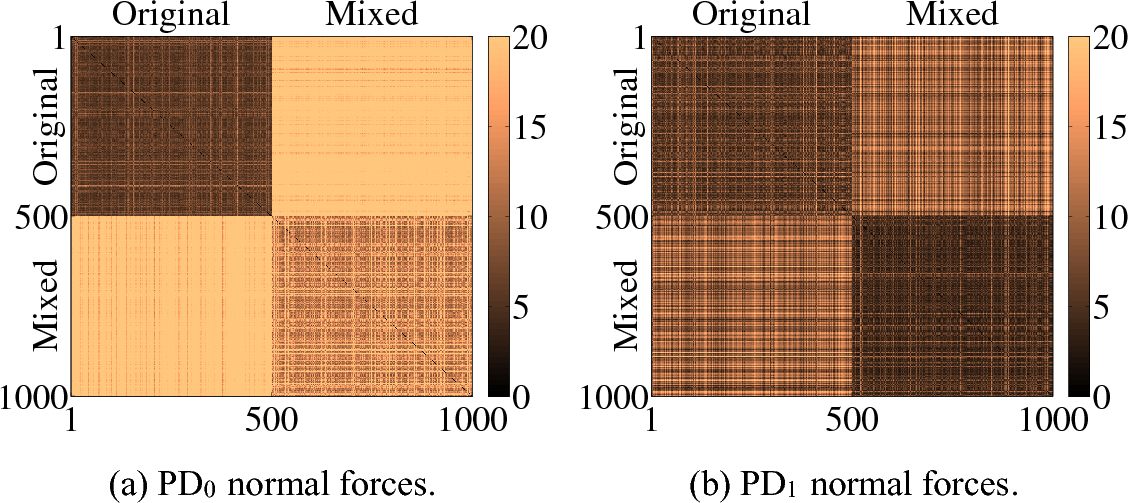
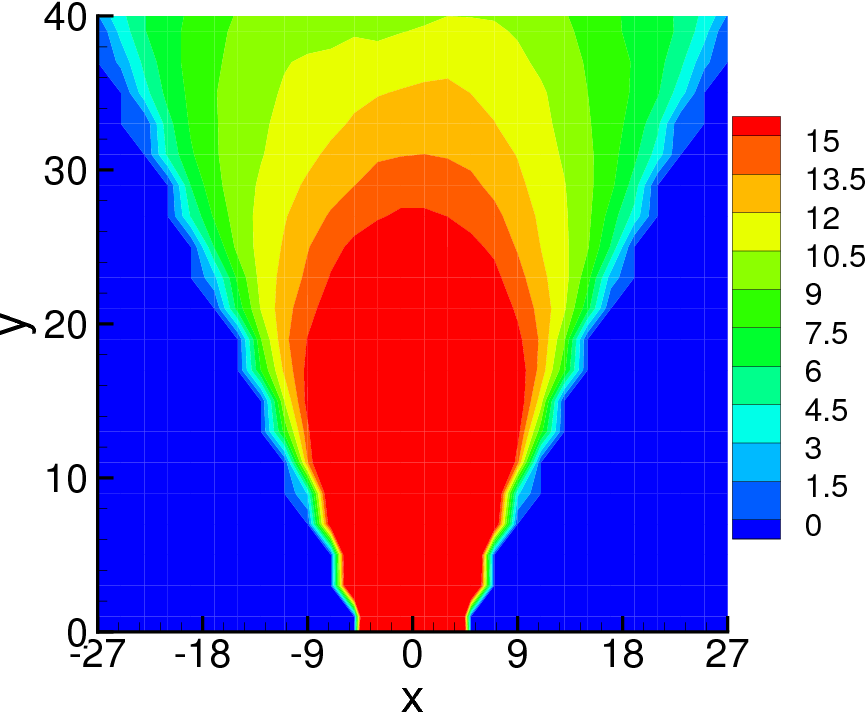
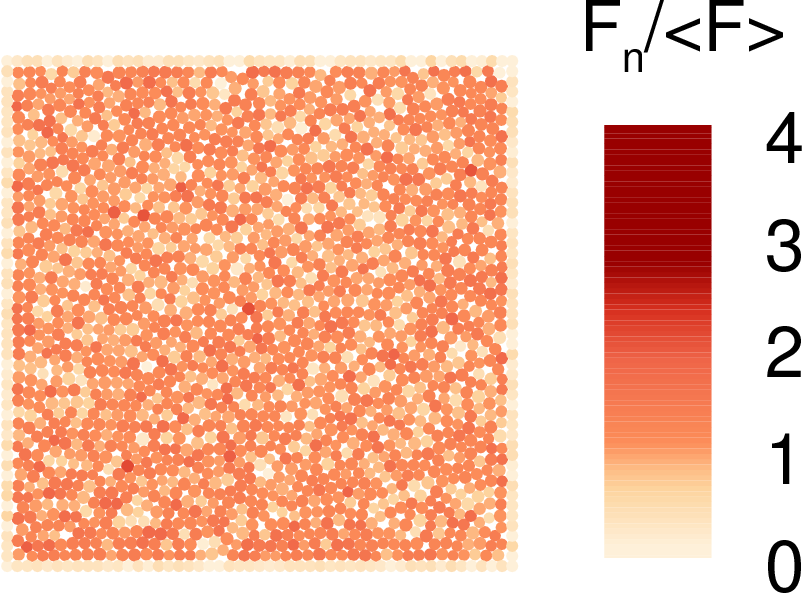
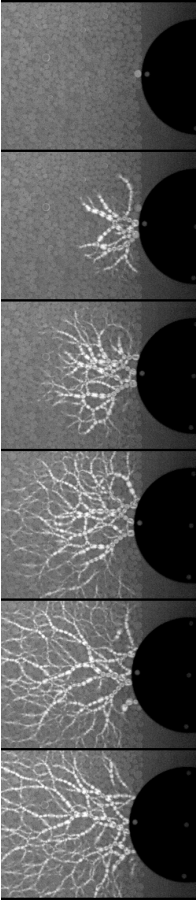
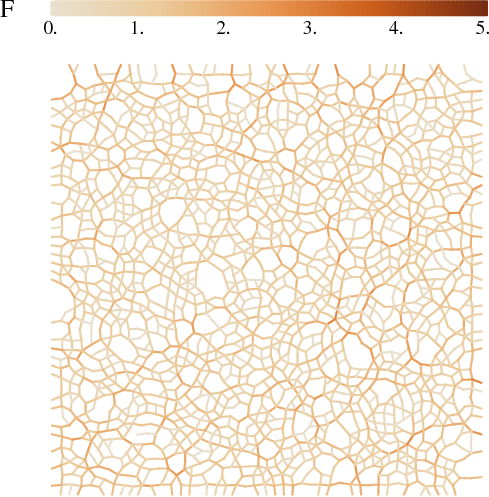
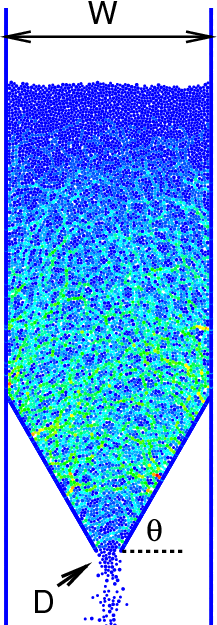
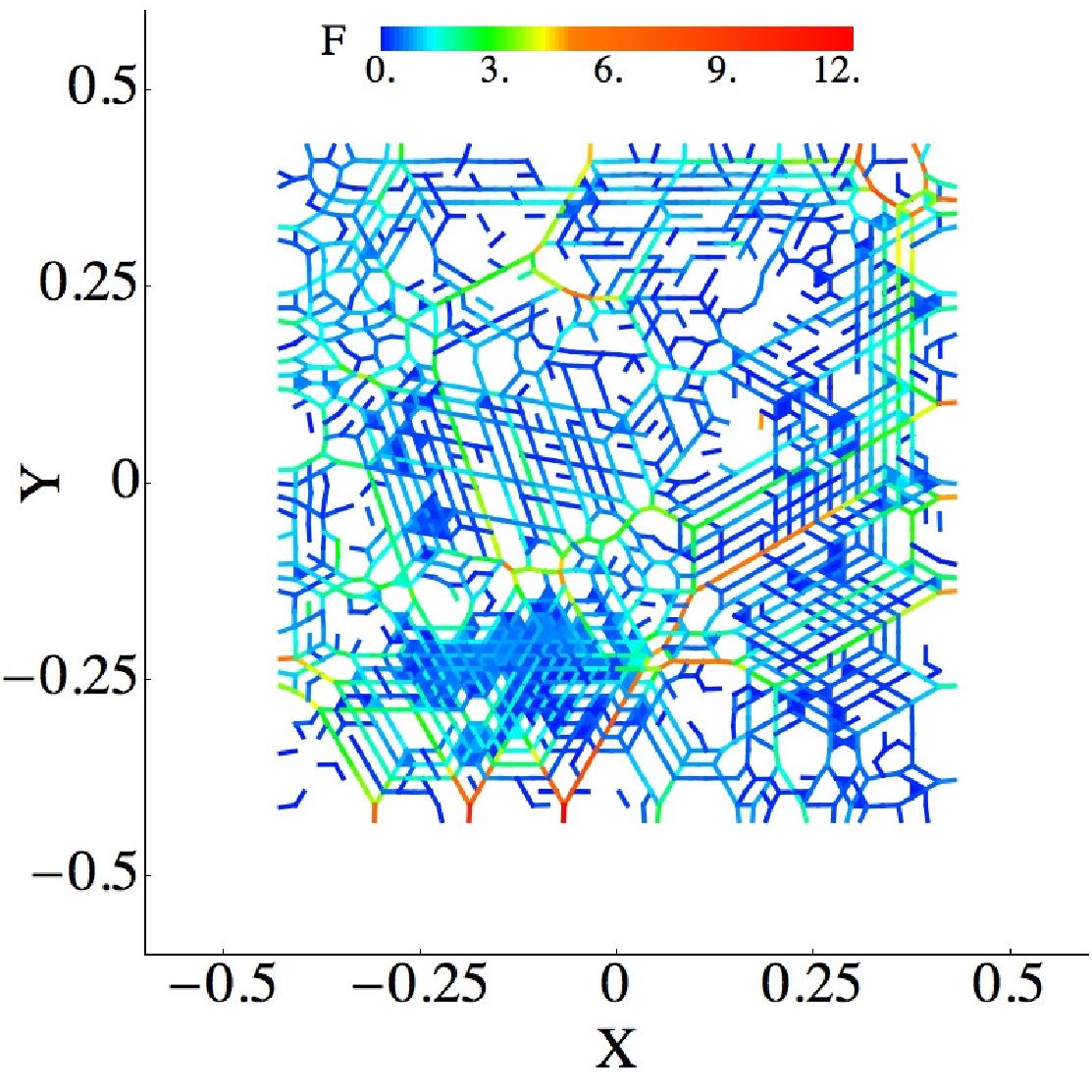
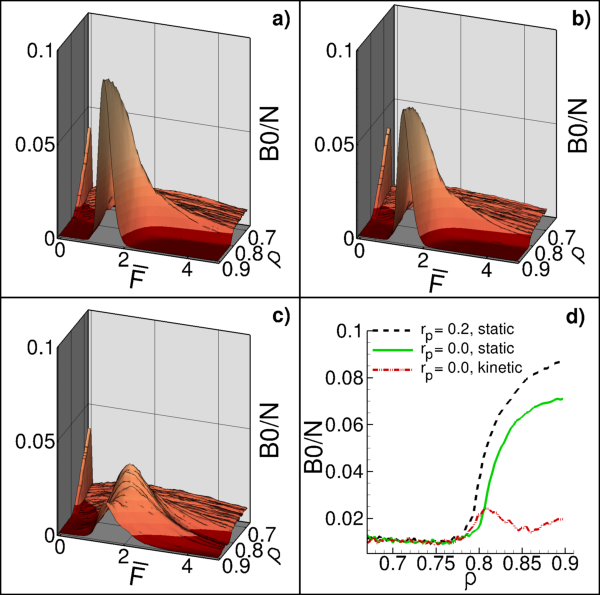
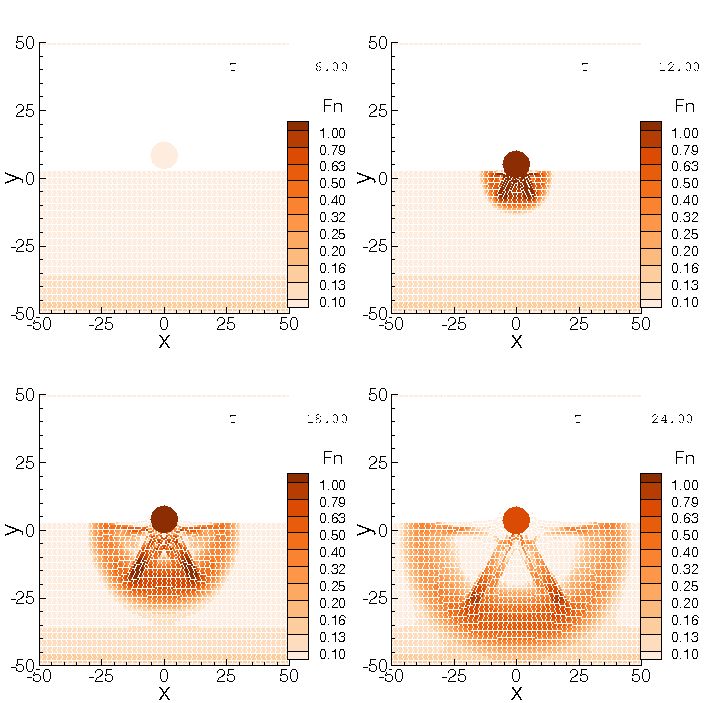
We consider two (2D) and three (3D) dimensional granular systems exposed to compression, and ask what is the influence of the number of physical dimensions on the properties of the interaction networks that spontaneously form as these systems evolve. The study is carried out based on discrete element simulations of frictional disks in 2D and spheres in 3D. Within the constraints of the considered simulation protocols, the main finding is that both the number of physical dimensions and the type of particle-particle interaction significantly influence the properties of interaction networks. These networks play an important role in bridging the microscale (particle size) and macroscale (system size), thus both aspects (the interaction model and dimensionality) are carefully considered. Our work uses a combination of tools and techniques, including percolation study, statistical analysis, as well as algebraic topology-based techniques. In many instances, different techniques and measures provide complementary information that, when combined, allow for gaining better insight into the properties of interaction networks in compressed particulate systems.

Animations: 1 2

R. Basak, R. Kozlowski, L.A. Pugnaloni, M. Kramar, J.E. Socolar, C.M. Carlevaro, and L. Kondic, Evolution of force networks during stick-slip motion of an intruder in a granular material: Topological measures extracted from experimental data, Phys. Rev. E, 108, 054903, (2023)

In quasi-two-dimensional experiments with photoelastic particles confined to an annular region, an intruder constrained to move in a circular path halfway between the annular walls experiences stick-slip dynamics. We discuss the response of the granular medium to the driven intruder, focusing on the evolution of the force network during sticking periods. Because the available experimental data do not include precise information about individual contact forces, we use an approach developed in our previous work [Basak et al., J. Eng. Mech. 147, 04021100 (2021)] based on networks constructed from measurements of the integrated strain magnitude on each particle. These networks are analyzed using topological measures based on persistence diagrams, revealing that force networks evolve smoothly but in a nontrivial manner throughout each sticking period, even though the intruder and granular particles are stationary. Characteristic features of persistence diagrams show identifiable slip precursors. In particular, the number of generators describing the structure and complexity of force networks increases consistently before slips. Key features of the dynamics are similar for granular materials composed of disks or pentagons, but some details are consistently different. In particular, we find significantly larger fluctuations of the measures computed based on persistence diagrams and, therefore, of the underlying networks, for systems of pentagonal particles.

P. Bretz, L. Kondic, and M. Kramar, Stochastic methods for slip prediction in a sheared granular system, Phys. Rev. E, 107, 054901, (2023)

We consider a sheared granular system experiencing intermittent dynamics of stick-slip type via discrete element simulations. The considered setup consists of a two-dimensional system of soft frictional particles sandwiched between solid walls, one of which is exposed to a shearing force. The slip events are detected using stochastic state space models applied to various measures describing the system. The amplitudes of the events spread over more than four decades and present two distinctive peaks, one for the microslips and the other for the slips. We show that the measures describing the forces between the particles provide earlier detection of an upcoming slip event than the measures based solely on the wall movement. By comparing the detection times obtained from the considered measures, we observe that a typical slip event starts with a local change in the force network. However, some local changes do not spread globally over the force network. For the changes that become global, we find that their size strongly influences the further behavior of the system. If the size of a global change is large enough, then it triggers a slip event; if it is not, then a much weaker microslip follows. Quantification of the changes in the force network is made possible by formulating clear and precise measures describing their static and dynamic properties.

L. A. Pugnaloni, C. M. Carlevaro, R. Kozlowski, H. Zheng, L. Kondic, J. E. S. Socolar, Universal features of the stick-slip dynamics of an intruder moving through a confined granular medium, Phys. Rev. E, 105, L042902, (2022)

Experiments and simulations of an intruder dragged by a spring through a two-dimensional annulus of granular material exhibit robust force fluctuations. At low packing fractions ( ϕ<ϕ0), the intruder clears an open channel. Above ϕ0, stick-slip dynamics develop, with an average energy release that is independent of the particle-particle and particle-base friction coefficients but does depend on the width W of the annulus and the diameter D of the intruder. A simple model predicts the dependence of ϕ0 on W and D, allowing for a data collapse for the average energy release as a function of ϕ/ϕ0 . These results pose challenges for theories of mechanical failure in amorphous materials.

M. Kramár, C. Cheng, R. Basak, and L. Kondic, On intermittency in sheared granular systems, Soft Matter, 18, 3583-3593, (2022)

We consider a system of granular particles{,} modeled by two dimensional frictional soft elastic disks{,} that is exposed to externally applied time-dependent shear stress in a planar Couette geometry. We concentrate on the external forcing that produces intermittent dynamics of stick-slip type. In this regime{,} the top wall remains almost at rest until the applied stress becomes sufficiently large{,} and then it slips. We focus on the evolution of the system as it approaches a slip event. Our main finding is that there are two distinct groups of measures describing system behavior before a slip event. The first group consists of global measures defined as system-wide averages at a fixed time. Typical examples of measures in this group are averages of the normal or tangent forces acting between the particles{,} system size and number of contacts between the particles. These measures do not seem to be sensitive to an approaching slip event. On average{,} they tend to increase linearly with the force pulling the spring. The second group consists of the time-dependent measures that quantify the evolution of the system on a micro (particle) or mesoscale. Measures in this group first quantify the temporal differences between two states and only then aggregate them to a single number. For example{,} Wasserstein distance quantitatively measures the changes of the force network as it evolves in time while the number of broken contacts quantifies the evolution of the contact network. The behavior of the measures in the second group changes dramatically before a slip event starts. They increase rapidly as a slip event approaches{,} indicating a significant increase in fluctuations of the system before a slip event is triggered.

S. Luding, K. Taghizadeh, C. Cheng, and L. Kondic, Understanding slow compression and decompression of frictionless soft granular matter by network analysis, Soft Matter, 18, 1868-1884, (2022)

We consider dense granular systems in three spatial dimensions exposed to slow compression and decompression, below, during, above and well above jamming. The evolution of granular systems under slow deformation is non-trivial and involves smooth, continuous, reversible (de)compression periods, interrupted by fast, discontinuous, irreversible transition events. These events are often, but not always, associated with rearrangements of particles and of the contact network. How many particles are involved in these transitions between two states can range from few to almost all in the system. An analysis of the force network that is built on top of the contact network is carried out using the tools of persistent homology. Results involve the observation that kinetic energy is correlated with the intensity of rearrangements, while the evolution of global mechanical measures, such as pressure, is strongly correlated with the evolution of the topological measures quantifying loops in the force network. Surprisingly, some transitions are clearly detected by persistent homology even though motion/rearrangement of particles is much weaker, i.e., much harder to detect or, in some cases, not observed at all.

R, Basak, C. M. Carlevaro, R. Kozlowski, C. Cheng, L. A. Pugnaloni, M. Kramár, H. Zheng, J. E. S. Socolar, and L. Kondic, Two Approaches to Quantification of Force Networks in Particulate Systems, J. Eng. Mech., 147, 04021100, (2021)

The interactions between particles in dense particulate systems are organized in force networks, mesoscale features that influence the macroscopic response to applied stresses. The detailed structure of these networks is, however, difficult to extract from experiments that cannot resolve individual contact forces. In this study, we showed that certain persistent homology (PH) measures extracted from data accessible to experiment are strongly correlated with the same features extracted from the full contact force network. We performed simulations known to accurately model experiments on an intruder being pushed through a two-dimensional (2D) granular layer and compared PH properties of full contact force networks and networks constructed using only the sum of the normal forces on each grain. We found that the main features were highly correlated, suggesting that data commonly available in experiments are sufficient for quantifying the structure of force networks in evolving granular systems.

M. Kramár, L. Kovalcinova, K. Mischaikow, and L. Kondic, Quantitative measure of memory loss in complex spatiotemporal systems, Chaos: An Interdisciplinary Journal of Nonlinear Science, 31, 033126, (2021)

History dependence of the evolution of complex systems plays an important role in forecasting. The precision of the predictions declines as the memory of the systems is lost. We propose a simple method for assessing the rate of memory loss that can be applied to experimental data observed in any metric space X. This rate indicates how fast the future states become independent of the initial condition. Under certain regularity conditions on the invariant measure of the dynamical system, we prove that our method provides an upper bound on the mixing rate of the system. This rate can be used to infer the longest time scale on which the predictions are still meaningful. We employ our method to analyze the memory loss of a slowly sheared granular system with a small inertial number I. We show that, even if I is kept fixed, the rate of memory loss depends erratically on the shear rate. Our study suggests the presence of bifurcations at which the rate of memory loss increases with the shear rate, while it decreases away from these points. We also find that the rate of memory loss is closely related to the frequency of the sudden transitions of the force network. Moreover, the rate of memory loss is also well correlated with the loss of correlation of shear stress measured at the system scale. Thus, we have established a direct link between the evolution of force networks and the macroscopic properties of the considered system.

C. Cheng, A. Z. Aghil, and L. Kondic, Correlating the force network evolution and dynamics in slider experiments, EPJ Web Conf., 249, 02007, (2021)

The experiments involving a slider moving on top of granular media consisting of photoelastic particles in two dimensions have uncovered elaborate dynamics that may vary from continuous motion to crackling, periodic motion, and stick-slip type of behavior. We establish that there is a clear correlation between the slider dynamics and the response of the force network that spontaneously develop in the granular system. This correlation is established by application of the persistence homology that allows for formulation of objective measures for quantification of time-dependent force networks. We find that correlation between the slider dynamics and the force network properties is particularly strong in the dynamical regime characterized by well-defined stick-slip type of dynamics.

L. Kondic, A. G. González, J. A. Diez, J. D. Fowlkes, and P. Rack, Liquid-State Dewetting of Pulsed-Laser-Heated Nanoscale Metal Films and Other Geometries, Annual Review of Fluid Mechanics, 52, 235-262, (2020)

Metal films of nanoscale thickness, deposited on substrates and exposed to laser heating, provide systems that involve several interesting multiphysics effects. In addition to fluid mechanical aspects associated with a free boundary setup, other relevant physical effects include phase change, thermal flow, and liquid–solid interactions. Such films are challenging to model, in particular because inertial effects may be relevant, and large contact angles require care when considering the long-wave formulation. Applications of nanoscale metal films are numerous, and the materials science community is actively pursuing more complex setups involving templated films and substrates, bimetallic films and alloys, and a variety of elemental film geometries. The goal of this review is to discuss our current understanding of thin metal film systems, while also providing an overview of the challenges in this research area, which stands at the intersection of fluid mechanics, materials science, and thermal physics.

S. Shah, C. Cheng, P. Jalali, and L. Kondic, Failure of confined granular media due to pullout of an intruder: from force networks to a system wide response, Soft Matter, 16, 7685, (2020)

We investigate computationally the pullout of a spherical intruder initially buried at the bottom of a granular column. The intruder starts to move out of the granular bed once the pulling force reaches a critical value, leading to material failure. The failure point is found to depend on the diameter of the granular column, pointing out the importance of particle–wall interactions in determining the material response. Discrete element simulations show that prior to failure, the contact network is essentially static, with only minor rearrangements of the particles. However, the force network, which includes not only the contact information, but also the information about the interaction strength, undergoes nontrivial evolution. An initial insight is obtained by considering the relative magnitudes of normal and tangential forces between the particles, and in particular the proportion of contacts that reach Coulomb threshold. More detailed understanding of the processes leading to failure is reached by the analysis of both spatial and temporal properties of the force network using the tools of persistent homology. We find that the forces between the particles undergo intermittent temporal variations ahead of the failure. In addition to this temporal intermittency, the response of the force network is found to be spatially dependent and influenced by proximity to the intruder. Furthermore, the response is modified signifi- cantly by the interaction strength, with the relevant measures describing the response showing differing behaviors for the contacts characterized by large interaction forces.

M. Gameiro, A. Singh, L. Kondic, K . Mischaikow, and J. F. Morris, Interaction network analysis in shear thickening suspensions, Physical Review Fluids, 5, 034307, (2020)

Dense frictional particulate suspensions in a viscous liquid undergo increasingly strong continuous shear thickening as the solid packing fraction, φ, increases above a critical volume fraction, and discontinuous shear thickening is observed for even higher packing fractions. Recent studies have related shear thickening to a transition from mostly lubri- cated to predominantly frictional contacts with the increase in stress, with the transition determined by overcoming a repulsive force. The rheology and networks of frictional forces from two- and three-dimensional simulations of shear-thickening suspensions are studied. These are analyzed using measures of the topology of the network, including tools of persistent homology. We observe that at low stress, the frictional interaction networks are predominantly quasilinear along the compression axis. With an increase in stress, the force networks become more isotropic, forming loops in addition to chainlike structures. The topological measures of Betti numbers and total persistence provide a compact means of describing the mean properties of the frictional force networks, and provide a link between macroscopic rheology and the microscopic interactions. A total persistence measure de- scribing the significance of loops in the force network structure, as a function of stress and packing fraction, shows behavior similar to that of relative viscosity, and displays a scaling law near the jamming fraction for both two- and three-dimensional systems considered. The total persistence measures for both dimensions are found to be very similar.

C. M. Carlevaro, R. Kozlowski, L. A. Pugnaloni, H. Zheng, J. E. Socolar, and L. Kondic, Intruder in a two-dimensional granular system: Effects of dynamic and static basal friction on stick-slip and clogging dynamics, Physical Review E, 101, 012909, (2020)

We present simulation results for an intruder pulled through a two-dimensional granular system by a spring using a model designed to mimic the experiments described by Kozlowski et al. [Phys. Rev. E 100, 032905 (2019)]. In that previous study the presence of basal friction between the grains and the base was observed to change the intruder dynamics from clogging to stick-slip. Here we first show that our simulation results are in excellent agreement with the experimental data for a variety of experimentally accessible friction coefficients governing interactions of particles with each other and with boundaries. We then use simulations to explore a broader range of parameter space, focusing on the friction between the particles and the base. We consider both static and dynamic basal friction coefficients, which are difficult to vary smoothly in experiments. The simulations show that dynamic friction strongly affects the stick-slip behavior when the coefficient is decreased below 0.1, while static friction plays only a marginal role.

Animation

R. Kozlowski, M. Carlevaro, K. Daniels, L. Kondic, L.A. Pugnaloni, J. Socolar, H. Zheng, and R. P. Behringer, Dynamics of a grain-scale intruder in a two-dimensional granular medium with and without basal friction, Physical Review E, 100, 032905, (2019)

We report on a series of experiments in which a grain-sized intruder is pushed by a spring through a two- dimensional granular material composed of photoelastic disks in a Couette geometry. We study the intruder dynamics as a function of packing fraction for two types of supporting substrates: A frictional glass plate and a layer of water for which basal friction forces are negligible. We observe two dynamical regimes: Intermittent flow, in which the intruder moves freely most of the time but occasionally gets stuck, and stick-slip dynamics, in which the intruder advances via a sequence of distinct, rapid events. When basal friction is present, we observe a smooth crossover between the two regimes as a function of packing fraction, and we find that reducing the interparticle friction coefficient causes the stick-slip regime to shift to higher packing fractions. When basal friction is eliminated, we observe intermittent flow at all accessible packing fractions. For all cases, we present results for the statistics of stick events, the intruder velocity, and the force exerted on the intruder by the grains. Our results indicate the qualitative importance of basal friction at high packing fractions and suggest a possible connection between intruder dynamics in a static material and clogging dynamics in granular flows.

L. Kondic, Energy propagation through dense granular systems, Granular Matter, 21, 85, (2019)

We discuss affine and non-affine components of particle dynamics in the context of energy propagation through dense granular matter as a consequence of externally imposed boundary perturbation. Earlier work (Kondic et al. in Phys Rev E 79:041304, 2009) has shown that the frequency and the wavenumber of the imposed perturbations strongly influence propagation, and in particular that the frequencies and wavenumbers that lead to well-defined propagation are limited from above. The present work shows that strong non-affine component of particle dynamics is associated with dispersion and loss of coherence.

L. Kovalcinova, S. Karmakar, M. Schaber, A.-L. Schuhmacher, M. Scheel, M. DiMichiel, M. Brinkmann, R. Seemann, and L. Kondic, Energy dissipation in sheared wet granular assemblies, Physical Review E, 98, 032905, (2018)

Energy dissipation in sheared dry and wet granulates is considered in the presence of an externally applied confining pressure. Discrete element simulations reveal that for sufficiently small confining pressures, the energy dissipation is dominated by the effects related to the presence of cohesive forces between the particles. The residual resistance against shear can be quantitatively explained by a combination of two effects arising in a wet granulate: (i) enhanced friction at particle contacts in the presence of attractive capillary forces and (ii) energy dissipation due to the rupture and reformation of liquid bridges. Coulomb friction at grain contacts gives rise to an energy dissipation which grows linearly with increasing confining pressure for both dry and wet granulates. Because of a lower Coulomb friction coefficient in the case of wet grains, as the confining pressure increases the energy dissipation for dry systems is faster than for wet ones.

J.A. Dijksman, L. Kovalcinova, J. Ren, R.P. Behringer, M. Kramar, K. Mischaikow, and L. Kondic, Characterizing granular networks using topological metrics, Physical Review E, 97, 042903, (2018)

We carry out a direct comparison of experimental and numerical realizations of the exact same granular system as it undergoes shear jamming. We adjust the numerical methods used to optimally represent the experimental settings and outcomes up to microscopic contact force dynamics. Measures presented here range from microscopic through mesoscopic to systemwide characteristics of the system. Topological properties of the mesoscopic force networks provide a key link between microscales and macroscales. We report two main findings: (1) The number of particles in the packing that have at least two contacts is a good predictor for the mechanical state of the system, regardless of strain history and packing density. All measures explored in both experiments and numerics, including stress-tensor-derived measures and contact numbers depend in a universal manner on the fraction of nonrattler particles, fNR . (2) The force network topology also tends to show this universality, yet the shape of the master curve depends much more on the details of the numerical simulations. In particular we show that adding force noise to the numerical data set can significantly alter the topological features in the data. We conclude that both fNR and topological metrics are useful measures to consider when quantifying the state of a granular system.

L. Kondic, M. Kramár, L. Kovalčinová, and K. Mischaikow, Evolution of force networks in dense granular matter close to jamming, EPJ Web Conf., 140, 15014, (2017)

When dense granular systems are exposed to external forcing, they evolve on the time scale that is typically related to the externally imposed one (shear or compression rate, for example). This evolution could be characterized by observing temporal evolution of contact networks. However, it is not immediately clear whether the force networks, defined on contact networks by considering force interactions between the particles, evolve on a similar time scale. To analyze the evolution of these networks, we carry out discrete element simulations of a system of soft frictional disks exposed to compression that leads to jamming. By using the tools of computational topology, we show that close to jamming transition, the force networks evolve on the time scale which is much faster than the externally imposed one. The presentation will discuss the factors that determine this fast time scale.

L. Kovalcinova, A. Goullet, and L. Kondic, Scaling properties of force networks for compressed particulate systems, Physical Review E, 93, 042903, (2016)

We consider, computationally and experimentally, the scaling properties of force networks in the systems of circular particles exposed to compression in two spatial dimensions. The simulations consider polydisperse and monodisperse particles, both frictional and frictionless, and in experiments we use monodisperse and bidisperse frictional particles. While for some of the considered systems we observe consistent scaling exponents describing the behavior of the force networks, we find that this behavior is not universal. In particular,we find that frictionless systems, independently of whether they partially crystallize under compression or not, show scaling properties that are significantly different compared to the frictional disordered ones. The findings of nonuniversality are confirmed by explicitly computing fractal dimension for the considered systems. The results of the physical experiments are consistent with the results obtained in simulations of frictional disordered systems.

A.H. Clark, L. Kondic, and R.P. Behringer, Steady flow dynamics during granular impact, Physical Review E, 93, 050901, (2016)

We study experimentally and computationally the dynamics of granular flow during impacts where intruders strike a collection of disks from above. In the regime where granular force dynamics are much more rapid than the intruder motion, we find that the particle flow near the intruder is proportional to the instantaneous intruder speed; it is essentially constant when normalized by that speed. The granular flow is nearly divergence free and remains in balance with the intruder, despite the latters rapid deceleration. Simulations indicate that this observation is insensitive to grain properties, which can be explained by the separation of time scales between intergrain force dynamics and intruder dynamics. Assuming there is a comparable separation of time scales, we expect that our results are applicable to a broad class of dynamic or transient granular flows. Our results suggest that descriptions of static-in-time granular flows might be extended or modified to describe these dynamic flows. Additionally, we find that accurate grain-grain interactions are not necessary to correctly capture the granular flow in this regime.

L.A. Pugnaloni, C.M. Carlevaro, M. Kramár, K. Mischaikow, and L. Kondic, Structure of force networks in tapped particulate systems of disks and pentagons. I. Clusters and loops, Physical Review E, 93, 062902, (2016)

The force network of a granular assembly, defined by the contact network and the corresponding contact forces, carries valuable information about the state of the packing. Simple analysis of these networks based on the distribution of force strengths is rather insensitive to the changes in preparation protocols or to the types of particles. In this and the companion paper [Kondic et al., Phys. Rev. E 93, 062903 (2016)], we consider two-dimensional simulations of tapped systems built from frictional disks and pentagons, and study the structure of the force networks of granular packings by considering network's topology as force thresholds are varied. We show that the number of clusters and loops observed in the force networks as a function of the force threshold are markedly different for disks and pentagons if the tangential contact forces are considered, whereas they are surprisingly similar for the network defined by the normal forces. In particular, the results indicate that, overall, the force network is more heterogeneous for disks than for pentagons. Such differences in network properties are expected to lead to different macroscale response of the considered systems, despite the fact that averaged measures (such as force probability density function) do not show any obvious differences. Additionally, we show that the states obtained by tapping with different intensities that display similar packing fraction are difficult to distinguish based on simple topological invariants.

L. Kondic, M. Kramár, L.A. Pugnaloni, C.M. Carlevaro, and K. Mischaikow, Structure of force networks in tapped particulate systems of disks and pentagons. II. Persistence analysis, Physical Review E, 93, 062903, (2016)

In the companion paper [Pugnaloni et al., Phys. Rev. E 93, 062902 (2016)], we use classical measures based on force probability density functions (PDFs), as well as Betti numbers (quantifying the number of components, related to force chains, and loops), to describe the force networks in tapped systems of disks and pentagons. In the present work, we focus on the use of persistence analysis, which allows us to describe these networks in much more detail. This approach allows us not only to describe but also to quantify the differences between the force networks in different realizations of a system, in different parts of the considered domain, or in different systems. We show that persistence analysis clearly distinguishes the systems that are very difficult or impossible to differentiate using other means. One important finding is that the differences in force networks between disks and pentagons are most apparent when loops are considered: the quantities describing properties of the loops may differ significantly even if other measures (properties of components, Betti numbers, force PDFs, or the stress tensor) do not distinguish clearly or at all the investigated systems.

P. Mort, J.N. Michaels, R.P. Behringer, C.S. Campbell, L. Kondic, M. Kheiripour Langroudi, M. Shattuck, J. Tang, G.I. Tardos, and C. Wassgren, Dense granular flow - A collaborative study, Powder Technology, 284, 571-584, (2015)

The International Fine Powder Research Institute (IFPRI) has funded an extensive program in dry powder and granular flows, including a focused study on dense flows of interest to a range of industrial handling and process unit operations, especially dense flows at relatively high shear rates. The dense flow program included experimental studies of granular rheology in 3D axial Couette and 2D hopper geometries, wherein the effect of force chains and jamming interactions were investigated as relevant to flow, stress and packing dynamics. The program cumulated in a collaborative study funded by the NSF, wherein a group of academic collaborators was invited to model experimental systems used in IFPRI-sponsored projects. This paper provides a summary of the IFPRI program, details of the collaborative modeling study, and perspective on what is needed to progress the work further.

L. Kovalcinova, A. Goullet, and L. Kondic, Percolation and jamming transitions in particulate systems with and without cohesion, Physical Review E, 92, 032204, (2015)

We consider percolation and jamming transitions for particulate systems exposed to compression. For the systems built of particles interacting by purely repulsive forces in addition to friction and viscous damping, it is found that these transitions are influenced by a number of effects, and in particular by the compression rate. In a quasistatic limit, we find that for the considered type of interaction between the particles, percolation and jamming transitions coincide. For cohesive systems, however, or for any system exposed to even slow dynamics, the differences between the considered transitions are found and quantified.

A.H. Clark, A.J. Petersen, L. Kondic, and R.P. Behringer, Nonlinear force propagation during granular impact, Physical Review Letters, 114, 144502, (2015)

We experimentally study nonlinear force propagation into granular material during impact from an intruder, and we explain our observations in terms of the nonlinear grain-scale force relation. Using highspeed video and photoelastic particles, we determine the speed and spatial structure of the force response just after impact.We show that these quantities depend on a dimensionless parameter, M' = t_c v₀/d, where v₀ is the intruder speed at impact, d is the particle diameter, and t_c is the collision time for a pair of grains impacting at relative speed v₀. The experiments access a large range of M by using particles of three different materials. When M' ≪ 1, force propagation is chainlike with a speed, v_f, satisfying v_f ∝ d=v_c. For larger M', the force response becomes spatially dense and the force propagation speed departs from v_f ∝ d=t_c, corresponding to collective stiffening of a strongly compressed packing of grain

M. Kramár, A. Goullet, L. Kondic, and K. Mischaikow, Evolution of force networks in dense particulate media, Physical Review E, 90, 052203, (2014)

We utilize the tools of persistent homology to analyze features of force networks in dense granular matter, modeled as a collection of circular, inelastic frictional particles. The proposed approach describes these networks in a precise and tractable manner, allowing us to identify features that are difficult or impossible to characterize by other means. In contrast to other techniques that consider each force threshold level separately, persistent homology allows us to consider all threshold levels at once to describe the force network in a complete and insightful manner. We consider continuously compressed system of particles characterized by varied polydispersity and friction in two spatial dimensions.We find significant differences between the force networks in these systems, suggesting that their mechanical response may differ considerably as well.

L. Kondic, Simulations of two dimensional hopper flow, Granular Matter, 16, 235-242, (2014)

We report on discrete element simulations of the flow out of a hopper. The geometry of the setup, as well as the material parameters, are taken directly from the exper- iments reported by Tang and Behringer (Chaos 21:041107, 2011; IFRPI-NSF collaboratory: 2D hopper data summary, 2010 ). The simulations consider flow of elastic, frictional, disk-like particles as the slope of the hopper walls and the sizeoftheopeningarevaried,sothatwecanconsiderboththe regime where jamming happens frequently (small openings) and where it occurs very rarely, or not at all (large openings), as well as the influence of the slope of hopper walls. We dis- cuss the distribution of jamming events, the mass flux out of the hopper, and the influence of material parameters on these quantities. In addition, we consider velocity and pres- sure fields in the hopper, as well as their fluctuations.

M. Kramár, A. Goullet, L. Kondic, and K. Mischaikow, Quantifying force networks in particulate systems, Physica D: Nonlinear Phenomena, 283, 37-55, (2014)

We present mathematical models based on persistent homology for analyzing force distributions in particulate systems. We define three distinct chain complexes of these distributions: >digital, position, and interaction, motivated by different types of data that may be available from experiments and simulations, e.g. digital images, location of the particles, and the forces between the particles, respectively. We describe how algebraic topology, in particular, homology allows one to obtain algebraic representations of the geometry captured by these complexes. For each complex we define an associated force network from which persistent homology is computed. Using numerical data obtained from discrete element simulations of a system of particles undergoing slow compression, we demonstrate how persistent homology can be used to compare the force distributions in different systems, and discuss the differences between the properties of digital, position, and interaction force networks. To conclude, we formulate well-defined measures quantifying differences between force networks corresponding to the different states of a system, and therefore allow to analyze in precise terms dynamical properties of force networks.

Animation

M. Kramar, A. Goullet, L. Kondic, and K. Mischaikow, Persistence of force networks in compressed granular media, Physical Review E, 87, 042207, (2013)

We utilize the tools of persistent homology to analyze features of force networks in dense granular matter, modeled as a collection of circular, inelastic frictional particles. The proposed approach describes these networks in a precise and tractable manner, allowing us to identify features that are difficult or impossible to characterize by other means. In contrast to other techniques that consider each force threshold level separately, persistent homology allows us to consider all threshold levels at once to describe the force network in a complete and insightful manner. We consider continuously compressed system of particles characterized by varied polydispersity and friction in two spatial dimensions. We find significant differences between the force networks in these systems, suggesting that their mechanical response may differ considerably as well.

L. Kondic, A. Goullet, C.S. O'Hern, M. Kramar, K. Mischaikow, and R.P. Behringer, Topology of force networks in compressed granular media, EPL(Europhysics Letters), 97, 54001, (2012)

Using numerical simulations, we investigate the evolution of the structure of force networks in slowly compressed model granular materials in two spatial dimensions. We quantify the global properties of the force networks using the zeroth Betti number B0, which is a topological invariant. We find that B0 can distinguish among force networks in systems with frictionless vs. frictional disks and varying size distributions. In particular, we show that 1) the force networks in systems composed of frictionless, monodisperse disks differ significantly from those in systems with frictional, polydisperse disks and we isolate the effect (friction, polydispersity) leading to the differences; 2) the structural properties of force networks change as the system passes through the jamming transition; and 3) the force network continues to evolve as the system is compressed above jamming, e.g., the size of connected clusters with forces larger than a given threshold decreases significantly with increasing packing fraction.

L. Kondic, X. Fang, W. Losert, C.S. O'Hern, and R.P. Behringer, Microstructure evolution during impact on granular matter, Physical Review E, 85, 011305, (2012)

We study the impact of an intruder on a dense granular material. The process of impact and interaction between the intruder and the granular particles is modeled using discrete element simulations in two spatial dimensions. In the first part of the paper we discuss how the intruder’s dynamics depends on (1) the intruder's properties, including its size, shape and composition, (2) the properties of the grains, including friction, polydispersity, structural order, and elasticity, and (3) the properties of the system, including its size and gravitational field. It is found that polydispersity and related structural order, and frictional properties of the granular particles, play a crucial role in determining impact dynamics. In the second part of the paper we consider the response of the granular system itself. We discuss the force networks that develop, including their topological evolution. The influence of friction and structural order on force propagation, including the transition from hyperbolic-like to elastic-like behavior is discussed, as well as the affine and nonaffine components of the grain dynamics. Several broad observations include the following: tangential forces between granular particles are found to play a crucial role in determining impact dynamics; both force networks and particle dynamics are correlated with the dynamics of the intruder itself.

Animations: 1 2

A.H. Clark, L. Kondic, and R.P. Behringer, Particle scale dynamics in granular impact, Physical Review Letters, 109, 238302, (2012)

We perform an experimental study of granular impact, where intruders strike 2D beds of photoelastic disks from above. High-speed video captures the intruder dynamics and the local granular force response, allowing investigation of grain-scale mechanisms in this process. We observe rich acoustic behavior at the leading edge of the intruder, strongly fluctuating in space and time, and we show that this acoustic activity controls the intruder deceleration, including large force fluctuations at short time scales. The average intruder dynamics match previous studies using empirical force laws, suggesting a new microscopic picture, where acoustic energy is carried away and dissipated.