Complex Flows and Soft Matter Group

Filtration

Membrane filters - essentially, thin sheets of porous material, which act to remove certain particles suspended in a fluid that passes through the medium - are in widespread industrial use, and represent a multi-billion dollar industry in the US alone. Major multinational companies manufacture a huge number of membrane-based filtration products, and maintain a keen interest in improving and optimizing their filters. Membrane filtration is used in applications as diverse as water purification; treatment of radioactive sludge; various purification processes in the biotech industry; and the cleaning of air and other gases. While the underlying applications and the details of the filtration may vary dramatically (gas vs liquid filtration; small vs large particle removal; slow vs fast throughput; rigid vs deformable particles), the broad engineering challenge of efficient filtration is the same: to achieve finely-controlled separation at low power consumption.

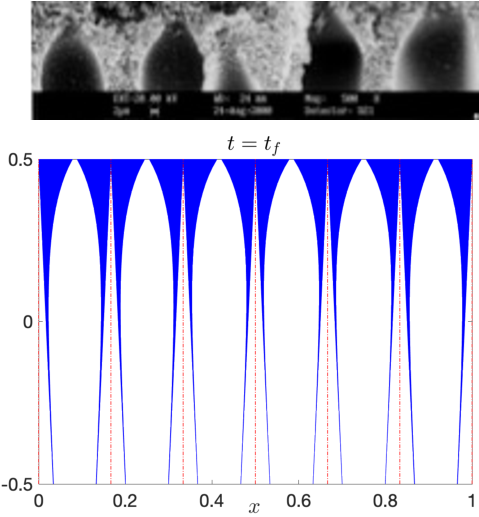
The desired separation control is to remove only those particles in a certain size range from the input flow (often referred to as "feed" or "challenge solution"); and the obvious resolution to the engineering challenge would appear to be: use the largest pore size and void fraction consistent with the separation requirement. However, these membrane characteristics (and hence the filter's behavior and performance) are far from constant over its lifetime: the particles removed from the feed are deposited within and on the membrane filter, fouling it and degrading the performance over time. The processes by which this fouling occurs are complex, and depend strongly on several factors, including: the internal structure of the membrane; the flow dynamics of the feed solution; and the type of particles in the feed (the shape, size, and chemistry affects how they are removed by the membrane).

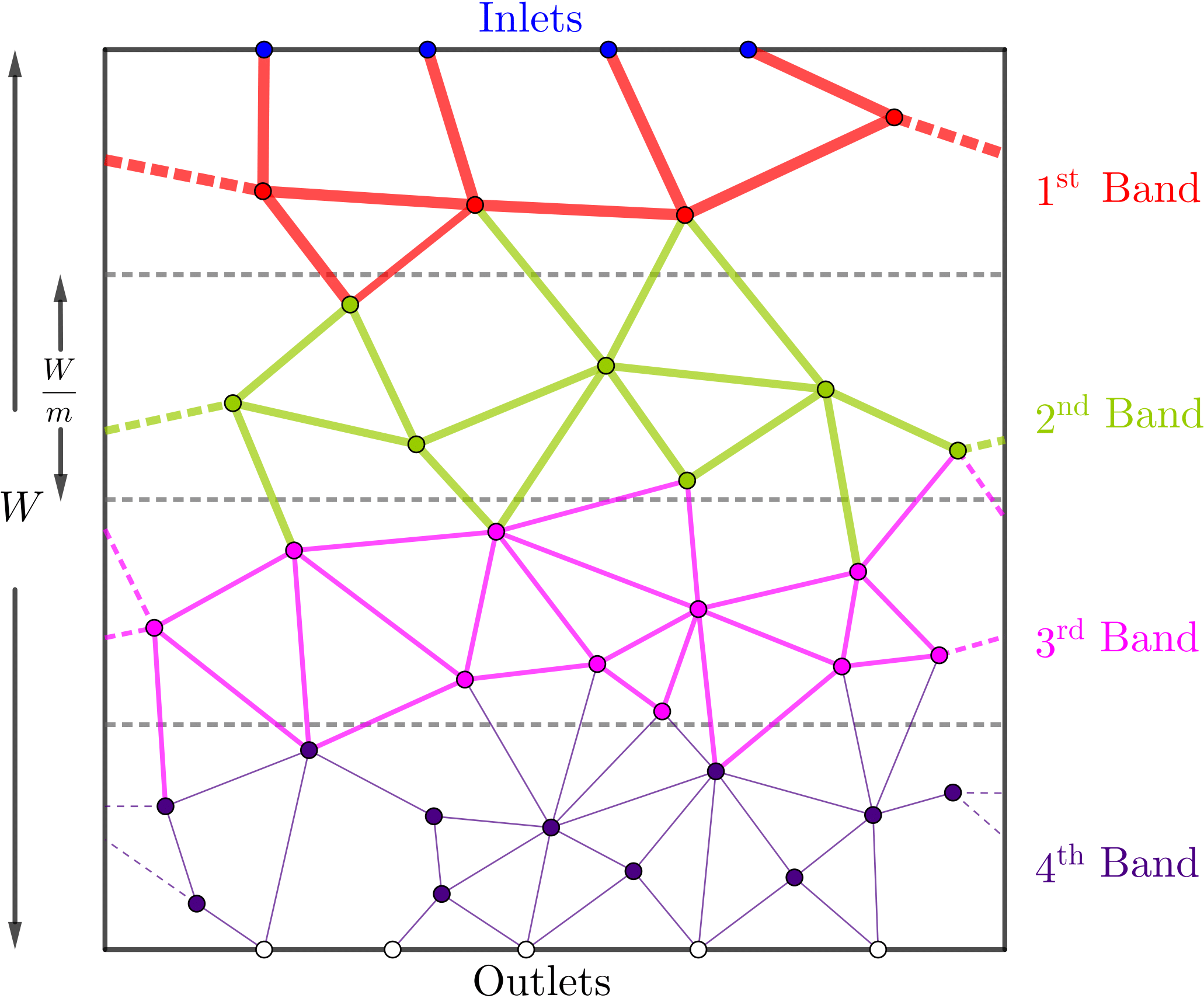
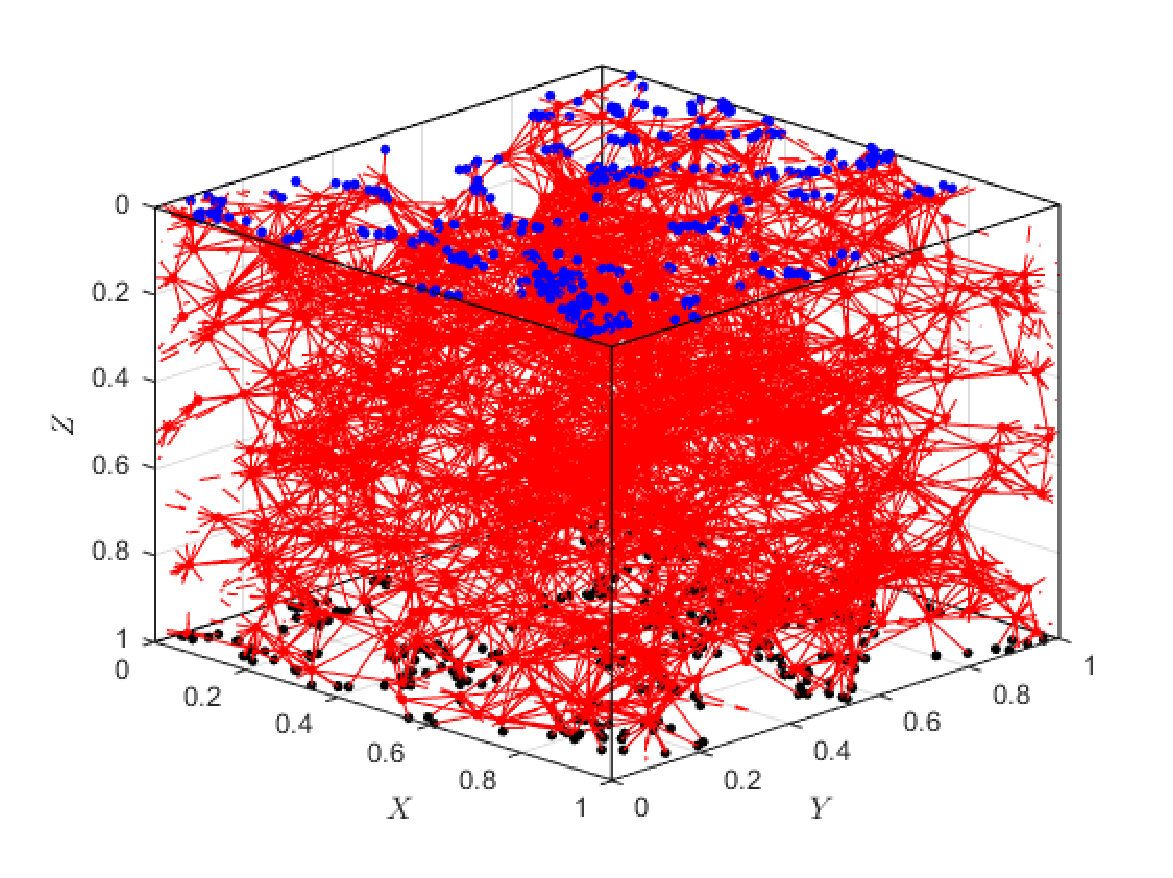
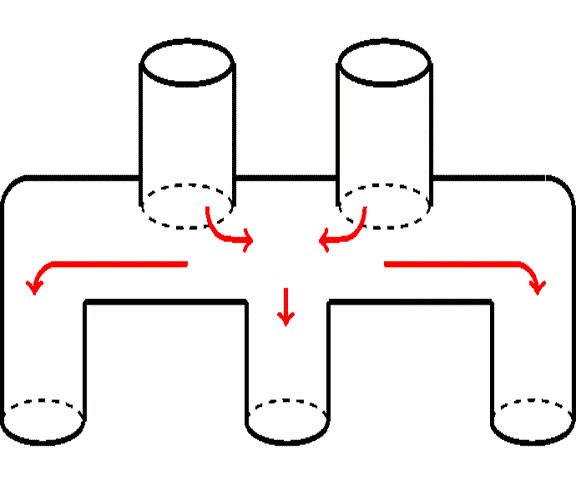
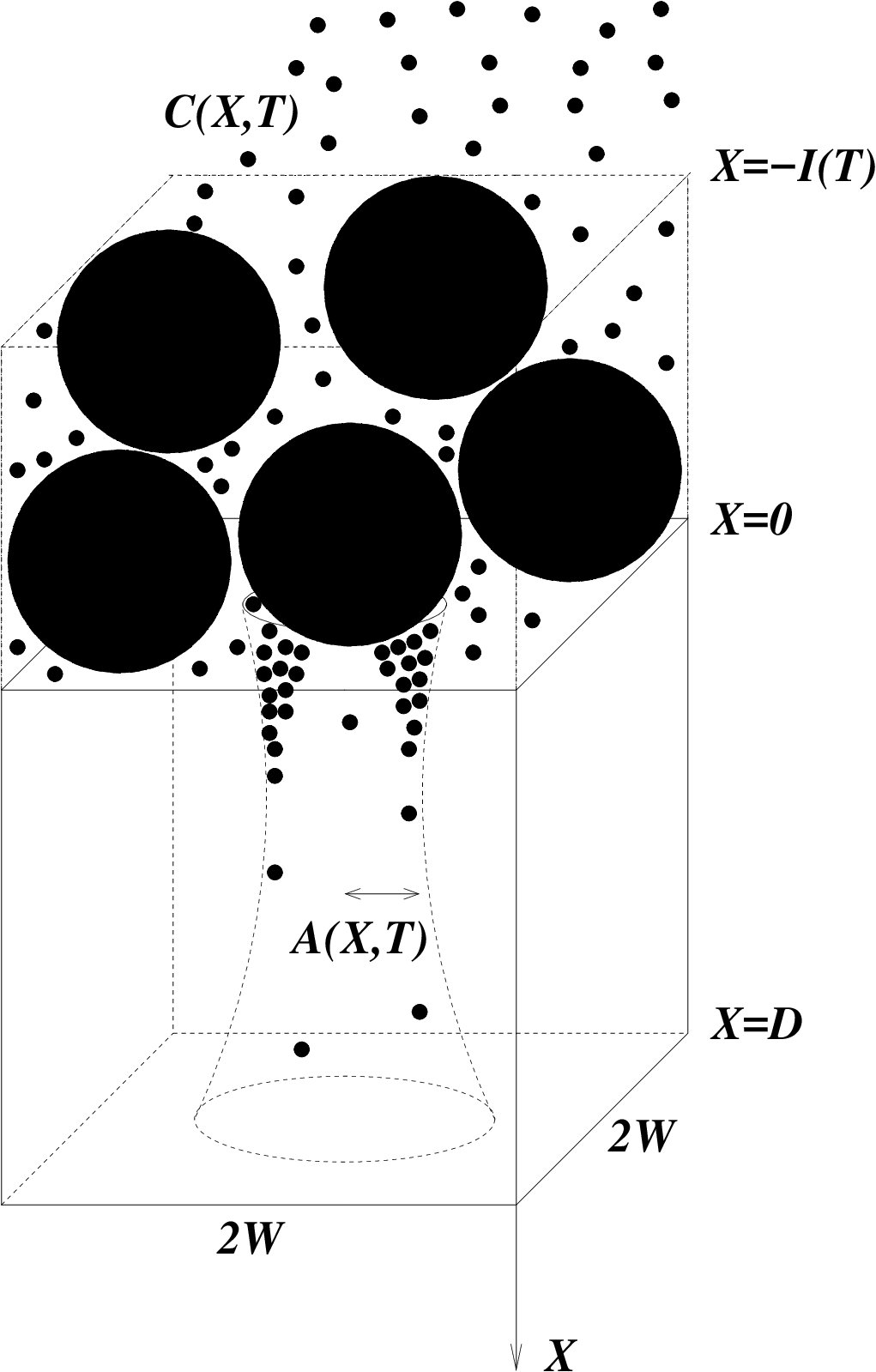
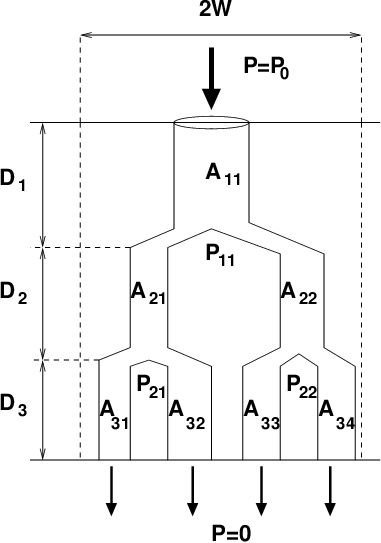
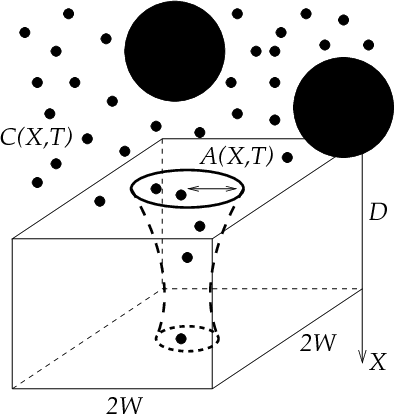
Our work is concerned with the development, analysis and computational simulation of new models governing membrane filtration, in two situations of widespread practical interest: (i) Flow and fouling within pleated filter cartridges; and (ii) Fouling models for internally heterogeneous membranes. In both scenarios we are building models that account for an arbitrary particle size distribution within the feed solution, and account also for a distribution of membrane pore sizes. First-principles theoretical studies of these scenarios should be of interest to those carrying out fundamental experimental research on such systems, as well as to those seeking to extend the scope of current applications and improve on manufacturing processes. This project has also served as a base for a joint research project with the group of local high school students from Middlesex County Academy for Science, Mathematics and Engineering Technologies in 2019: Anay Badiani, Sid Kunisetty, Justin Lee, and Heer Patel, leading to the research report linked here. Our recent publications in this area, listed below, give an indication of projects completed to date. This work is supported by the National Science Foundation under grants DMS-1261596 and DMS-1615719.

Recent Publications



B. Gu, L. Kondic, and L. J. Cummings, Flow through pore-size graded membrane pore network, Phys. Rev. Fluids, 8, 044502, (2023)





Pore-size gradients are often used in the design of membrane filters to increase filter lifetime and ensure fuller use of the initial membrane pore volume. In this work, we impose pore-size gradients in the setting of a membrane filter with an internal network of interconnected tubelike pores. We model the flow and foulant transport through the filter using the Hagen-Poiseuille framework coupled with advection equations via conservation of fluid and particle flux, with adsorption as the sole fouling mechanism. We study the influence of pore-size gradient on performance measures such as total filtrate throughput and accumulated contaminant concentration at the membrane downstream pore outlets. Within the limitations of our modeling assumptions we find that there is an optimal pore-radius gradient that maximizes filter efficiency independent of maximum pore length (an input parameter that influences the structure of the pore network), and that filters with longer characteristic pore length perform better.

B. Gu; L. Kondic; and L.J. Cummings, Network-based membrane filters: Influence of network and pore size variability on filtration performance, Journal of Membrane Science, 657, 120668, (2022)





We model porous membrane filters as networks of connected cylindrical pores via a random network generation protocol, and their initial pore radii via a uniform distribution of widths that vary about some mean value. We investigate the influence of network and pore size (radius) variations on the performance of membrane filters that undergo adsorptive fouling. We find that membrane porosity variations, independently of whether induced by variations of the pore radii or of the random pore network, are an important factor determining membrane filter performance. Network and pore size variations still play a role, in particular if pore radii variations are significant. To quantify the influence of these variations, we compare the performance metrics of networks built from pores of variable radii to their (equal porosity) counterparts built from pores of uniform radius. We show that the effect of pore radii variations is to increase throughput, but also to reduce foulant control.

B. Gu, D. Renaud, P. Sanaei, L. Kondic, and L. J. Cummings, On the influence of pore connectivity on performance of membrane filters, Journal of Fluid Mechanics, 902, A5, (2020)





We study the influence of a membrane filter's internal pore structure on its flow and adsorptive fouling behaviour. Membrane performance is measured via 1) comparison between volumetric flow rate and throughput during filtration; and 2) control of concentration of foulants at membrane pore outlets. Taking both measures into account, we address the merits and drawbacks of selected membrane pore structures. We first model layered planar membrane structures with intra-layer pore connections, and present comparisons between non-connected and connected structures. Our model predicts that membrane filters with connected pore structures lead to higher total volumetric throughput than those with non-connected structures, over the filter lifetime. We also provide a sufficient criterion for the concentration of particles escaping the filter to achieve a maximum in time (indicative of a membrane filter whose particle retention capability can deteriorate). Additionally, we find that the influence of intra-layer heterogeneity in pore-size distribution on filter performance, depends on the connectivity properties of the pores.

Y. Sun, P. Sanaei, L. Kondic, and L. J. Cummings, Modeling and design optimization for pleated membrane filters, Physical Review Fluids, 5, 044306, (2020)





Pleated membrane filters, which offer larger surface area to volume ratios than unpleated membrane filters, are used in a wide variety of applications. However, the performance of the pleated filter, as characterized by a flux-throughput plot, indicates that the equivalent unpleated filter provides better performance under the same pressure drop. Earlier work [Sanaei, Richardson, Witelski, and Cummings, J. Fluid Mech. 795, 36 (2016)] used a highly simplified membrane model to investigate how the pleating effect and membrane geometry affect this performance differential. In this work, we extend this line of investigation and use asymptotic methods to couple an outer problem for the flow within the pleated structure to an inner problem that accounts for the pore structure within the membrane. We use our model to formulate and address questions of optimal membrane design for a given filtration application.

Animation

P. Sanaei and L.J. Cummings, Membrane filtration with multiple fouling mechanisms, Physical Review Fluids, 4, 124301, (2019)





Manufacturers of membrane filters have an interest in optimizing the internal pore structure of the membrane to achieve the most efficient filtration. As filtration occurs, the membrane becomes fouled by impurities in the feed solution, and any effective model of filter performance must account for this. In this paper, we present a simplified mathematical model, which (i) characterizes membrane internal pore structure via permeability or resistance gradients in the depth of the membrane; (ii) accounts for multiple membrane fouling mechanisms (adsorption, blocking, and cake formation); (iii) defines a measure of filter performance; and (iv) for given operating conditions, is able to predict the optimum permeability or resistance profile for the chosen performance measure.

P. Sanaei and L.J. Cummings, Membrane filtration with complex branching pore morphology, Physical Review Fluids, 3, 094305, (2018)





Membrane filters are in widespread industrial use, and mathematical models to predict their efficacy are potentially very useful, as such models can suggest design modifications to improve filter performance and lifetime. Many models have been proposed to describe particle capture by membrane filters and the associated fluid dynamics, but most such models are based on a very simple structure in which the pores of the membrane are assumed to be simple circularly cylindrical tubes spanning the depth of the membrane. Real membranes used in applications usually have much more complex geometry, with interconnected pores that may branch and bifurcate. Pores are also typically larger on the upstream side of the membrane than on the downstream side. We present an idealized mathematical model, in which a membrane consists of a series of bifurcating pores, which decrease in size as the membrane is traversed. Feed solution is forced through the membrane by applied pressure and particles are removed from the feed by adsorption within pores (which shrinks them). Thus, the membrane?s permeability decreases as the filtration progresses. We discuss how filtration efficiency depends on the characteristics of the idealized branching structure.

P. Sanaei, and L.J. Cummings, Flow and fouling in membrane filters: effects of membrane morphology, Journal of Fluid Mechanics, 818, 744, (2017)





Membrane filters are used extensively in microfiltration applications. The type of membrane used can vary widely depending on the particular application, but broadly speaking the requirements are to achieve fine control of separation, with low power consumption. The solution to this challenge might seem obvious: select the membrane with the largest pore size and void fraction consistent with the separation requirements. However, membrane fouling (an inevitable consequence of successful filtration) is a complicated process, which depends on many parameters other than membrane-pore size and void fraction; and which itself greatly affects the filtration process and membrane functionality. In this work we formulate mathematical models that can (i) account for the membrane internal morphology (internal structure, pore size and shape, etc.); (ii) describe fouling of membranes with specific morphology; and (iii) make some predictions as to what type of membrane morphology might offer optimum filtration performance.

P. Sanaei, G.W. Richardson, T. Witelski, and L.J. Cummings, Flow and fouling in a pleated membrane filter, Journal of Fluid Mechanics, 795, 36-59, (2016)





Pleated membrane filters are widely used in many applications, and offer significantly better surface area to volume ratios than equal-area unpleated membrane filters. However, their filtration characteristics are markedly inferior to those of equivalent unpleated membrane filters in dead-end filtration. While several hypotheses have been advanced for this, one possibility is that the flow field induced by the pleating leads to spatially non-uniform fouling of the filter, which in turn degrades performance. In this paper we investigate this hypothesis by developing a simplified model for the flow and fouling within a pleated membrane filter. Our model accounts for the pleated membrane geometry (which affects the flow), for porous support layers surrounding the membrane, and for two membrane fouling mechanisms: (i) adsorption of very small particles within membrane pores; and (ii) blocking of entire pores by large particles. We use asymptotic techniques based on the small pleat aspect ratio to solve the model, and we compare solutions to those for the closest-equivalent unpleated filter.